Geometric Decomposition of H(div) Finite Element

Previously we use Lagrange elements as an example to introduce the simplicial lattice and construction of finite elements based on a decomposition of the simplicial lattice; see Simplicial Lattice and Lagrange Elements. In this post, we shall extend to H(div) conforming finite elements.

Reference: Section 4 of Geometric Decompositions of Div-Conforming Finite Element Tensors. Long Chen and Xuehai Huang. arXiv. 2021.

To leave comments (in math), please visit my UCI blog

Vector Lagrange Elements

Generalization of scalar Lagrange elements to vector Lagrange elements is straightforward. Just take $n$-copies of scalar functions. When we expand the vector into $n$-components, a fixed orthonormal basis is implicitly assumed.

Here the change of notation from $\mathbb T^f$​ to $\mathbb B_r^f(T)$ indicates the tangential component contributes to the bubble function space. ​

The coordinate can vary and non-orthonormal. We choose different and in general non-orthonormal basis adapted to each sub-simplex $f$​ to modify the geometric decomposition. The coordinate at $f$ is divided into tangential and normal parts.

Geometric Decomposition of H(div) Elements

Verification of \(\mathbb B_{r}^f(T) \subseteq \mathbb B_{r}({\rm div},T)\) is straight forward. For face $F$​​ not containing $f$​​, $b_f|_F = 0.$​

For face $F$​​​​​​ containing $f$​​​​ ​​, ${\rm tr} \boldsymbol u = \boldsymbol n_F \cdot \boldsymbol u = 0$​​​​ as $\boldsymbol n_F\cdot \boldsymbol t_i^f = 0$​​​​​. Therefore $\oplus_{\ell = 1}^n\oplus_{f\in \Delta_{\ell}(T)} \mathbb B_r^f( T)\subseteq \mathbb B_r({\rm div} , T)$​​​​​.

Then apply the trace operator to the decomposition and use ${\rm tr} \mathbb{B}^f_r(T ) = 0$​​​ to obtain \({\rm tr} \left ( \oplus _{\ell = 0}^{n-1}\oplus _{f\in \Delta_{\ell}(T)} \mathbb{N}^f_r( T)\right ) = {\rm tr} \mathbb P_r(T; \mathbb E^n).\) So the map tr is onto.

Now we prove it is also injective. Take a function $\boldsymbol u=\sum\limits_{\ell = 0}^{n-1}\sum\limits_{f\in \Delta_{\ell}(T)}\boldsymbol u_r^f $ with $\boldsymbol u_r^f \in \mathbb{N}^f_r(T)$ and ${\rm tr} \boldsymbol u = 0.$ We will prove $\boldsymbol u = 0$ by induction.

Since $\boldsymbol u(\texttt{v}_i)=\boldsymbol u_r^{\texttt{v}_i}(\texttt{v}_i)$ for $i=0,\ldots, n$, we get from ${\rm tr} \boldsymbol u = 0$ that $\boldsymbol u_r^{\texttt{v}_i}=\boldsymbol 0 $. Assume $\boldsymbol u_r^f=\boldsymbol 0 $ for all $f \in \Delta(T)$ whose dimension is less than $j$ with $1\leq j<n$. Then \(\boldsymbol u=\sum\limits_{\ell = j}^{n-1}\sum\limits_{f\in \Delta_{\ell}(T)}\boldsymbol u_r^f.\) Take $f\in \Delta_j(T)$. We have $\boldsymbol u|_f=\boldsymbol u_r^f|_f\in\mathbb{N}^f_r(T)$. Hence $(\boldsymbol u_r^f\cdot\boldsymbol n)|_f=(\boldsymbol u\cdot\boldsymbol n)|_f=0$ for any $\boldsymbol n\in\mathbb N_0^f$, which results in $\boldsymbol u_r^f=\boldsymbol 0 $. Therefore $\boldsymbol u = \boldsymbol 0 $.

Once we have proved the map tr is bijective, we get the bubble decomposition from the decomposition for the vector Lagrange elements.

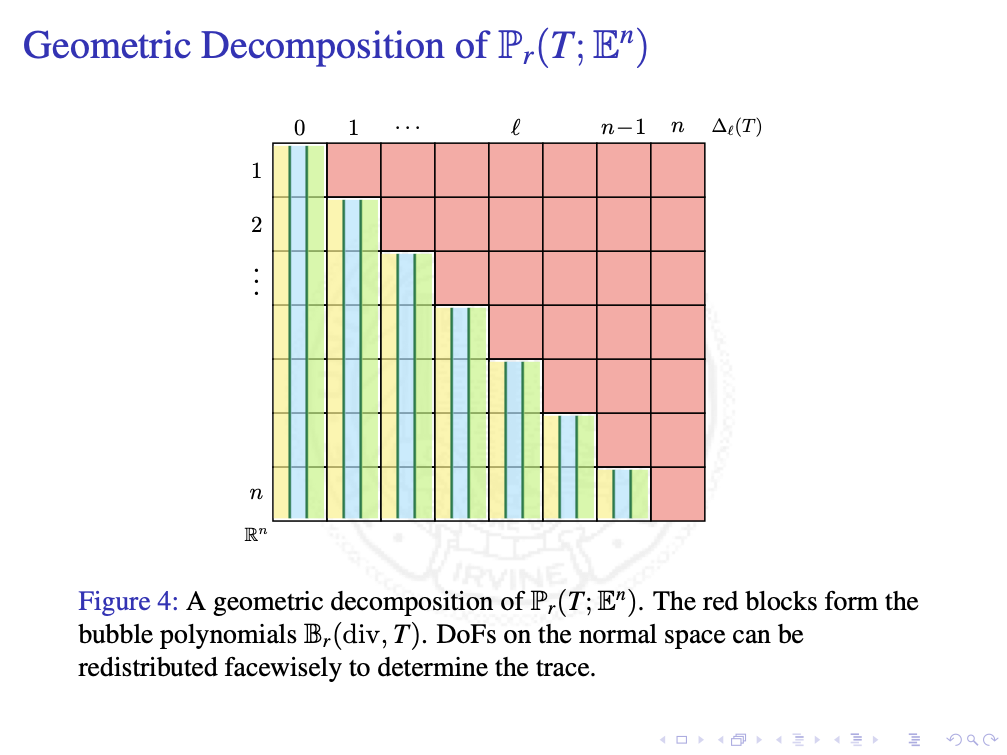
At each sub-simplex $f$​​, we can divide the vector into two parts: tangential and normal compnents. The tangential component consists of all div bubbles. The normal componet will determine the trace.

We use DoFs to glue the loal shape function to the global one. If the DoFs depends only on $f$ not the element containing $f$, we call it global, otherwise local. If we choose global normal basis at each $f$, we obtain a vector function which is continuous on the normal plane of each sub-simplex. In particular, it is continuous on the normal direction of $n-1$ face $F$ and thus H(div)-conforming.

All tangential components are considered as local. This is the main difference with the vector Lagrange elements which is continuous for all components.

Examples

We can construct several H(div) finite elements by different choices of the $t-n$​​ basis. The first example is BDM element. The normal basis ${\boldsymbol n_F, f\subseteq F\in \partial T}$​​ is local but the DoFs can be redistributed to each face $F$​ .

• F. Brezzi, J. Douglas, and L. D. Marini. Two families of mixed finite elements for second order elliptic problems. Numer. Math., 47(2):217–235, 1985.

DoFs on the normal space can be redistributed according to the following combinatory identity \((n-\ell) { n+1 \choose \ell+1} =(n+1) {n \choose \ell + 1}.\)

• On the left, there are ${ n+1 \choose \ell+1}$ $\ell$-dimensional sub-simplex $f$ in $\Delta_{\ell}(T)$ and each $f$ has $n - \ell$ normal vectors.
• On the right, there are $n+1$ faces $F\in \Delta_{n-1}(T)$ and each $F$ will have ${n \choose \ell + 1}$ $\ell$-dimensional sub-simplex $f$.

We can distribute $n-\ell$ copies of DoFs on an $\ell$-dimensional $f$ to each face $F$ to determine the trace $\boldsymbol n_F\cdot \boldsymbol v\in \mathbb P_r(F)$.

We have the geometric decomposition of the global BMD element space \(\begin{align*} V_{\small \rm BDM} = &\oplus_{F\in \Delta_{n-1}(\mathcal T_h)} \oplus_{\ell = 0}^{n-1}\oplus_{f\in \Delta_{\ell}(F)} \mathbb N^f_r(F, \Omega)\\ &\oplus \oplus_{T\in \mathcal T_h} \oplus_{\ell = 1}^n\oplus_{f\in \Delta_{\ell}(T)} \mathbb B^f_r(T, \Omega) \end{align*}\)

and \(\dim V_{\small \rm BDM} = |\Delta_{n-1}(\mathcal T_h)| { n + r -1 \choose r} + |\Delta_n(\mathcal T_h)| \sum_{\ell=1}^n{n+1 \choose \ell +1} \ell {r-1 \choose \ell}.\) Here \(\begin{align*} \mathbb N^f_r(F, \Omega):=&\{\boldsymbol v_h\in H({\rm div}, \Omega): \boldsymbol v_h|_T\in\mathbb N^f_r(T)\; \textrm{ for } T\in\mathcal T_h, F\subseteq T, \\ &\qquad\qquad\qquad\qquad\qquad\, \boldsymbol v_h|_{T'}=\boldsymbol 0 \;\textrm{ for } T'\in\mathcal T_h, F\not\subseteq T'\},\\ \mathbb B^f_r(T, \Omega):=&\{\boldsymbol v_h\in H({\rm div}, \Omega): \boldsymbol v_h|_T\in\mathbb B^f_r(T), \, \boldsymbol v_h|_{T'}=\boldsymbol 0 \;\textrm{ for } T'\in\mathcal T_h\backslash\{T\}\}. \end{align*}\)

When $k=0$​, it is the original Stenberg’s element [Stenberg 2010], i.e., only continuous at vertices. When $k = n-2$​, it is the generalization of H(div) element constructed in [CHH2018]. We allow $k=-1$​​ to include the BDM element.

• R. Stenberg. A nonstandard mixed finite element family. Numerische Mathematik, 115(1):131–139, Mar. 2010
• S. H. Christiansen, J. Hu, and K. Hu. Nodal finite element de Rham complexes. Numerische Mathematik, 139(2):411–446, June 2018

We have the geometric decomposition of the global Stenberg element space \(\begin{align*} V_{\small \rm Stenberg}^r &= \oplus_{\ell = 0}^{k}\oplus_{f\in \Delta_{\ell}(\mathcal T_h)} \mathbb N^f_r(\Omega) \oplus \oplus_{F\in \Delta_{n-1}(\mathcal T_h)}\oplus_{\ell = k+1}^{n-1}\oplus_{f\in \Delta_{\ell}(F)} \mathbb N^f_r(F, \Omega) \\ &\quad \oplus \oplus_{T\in \mathcal T_h} \oplus_{\ell = 1}^n\oplus_{f\in \Delta_{\ell}(T)} \mathbb B^f_r(T, \Omega) \end{align*}\)

and \(\begin{align*} \dim V_{\small \rm Stenberg}^r& = \sum_{\ell = 0}^{k}|\Delta_{\ell}(\mathcal T_h)| (n - \ell ){ r-1 \choose \ell} + |\Delta_{n-1}(\mathcal T_h)| \sum_{\ell = k+1}^{n-1}{n \choose \ell +1} {r-1 \choose \ell} \\ &\quad + |\Delta_n(\mathcal T_h)|\sum_{\ell=1}^n {n+1 \choose \ell +1} \ell {r-1 \choose \ell}. \end{align*}\)

Here \(\begin{align*} \mathbb N^f_r(\Omega):=&\{\boldsymbol v_h\in H({\rm div}, \Omega): \boldsymbol v_h|_T\in\mathbb N^f_r(T)\; \textrm{ for } T\in\mathcal T_h, f\subseteq T, \\ &\qquad\qquad\qquad\qquad\qquad\, \boldsymbol v_h|_{T'}=\boldsymbol 0 \;\textrm{ for } T'\in\mathcal T_h, f\not\subseteq T'\}. \end{align*}\)

Clearly \(V_{\small \rm Stenberg}^r\subseteq V_{\small \rm BDM}, \quad \dim V_{\small \rm Stenberg}^r<\dim V_{\small \rm BDM}.\)

Discrete inf-sup Condition

The continuity at normal planes introduces some constraint and make the discrete inf-sup condition harder.

The $t-n$ basis is used for two purpose:

1. a div-conforming element;
2. the discrete inf-sup condition.

If the div-conformity is the only concern, we can simply choose the Lagrange element. There is another consideration from the inf-sup condition.

In the continuous level, we have the inf-sup condition that ${\rm div} : H({\rm div} , \Omega)\to L^2(\Omega)$ is surjective and has a continuous right inverse. A regular potential also exists.

Theorem 1.1 in [CostabelMcIntosh2010]

Given a function $p\in L^2(\Omega)$​, there exists a $\boldsymbol u\in H^1(\Omega; \mathbb R^n)$​ s.t. ${\rm div} \boldsymbol u = p$ and $|\boldsymbol u|_1\lesssim | p|$​.

• M. Costabel and A. McIntosh. On Bogovski ̆ı and regularized Poincare ́ integral operators for de Rham com- plexes on Lipschitz domains. Math. Z., 265(2):297–320, 2010.

By the Euler’s formula for homogenous degree polynomials $\mathbb H_{r-1}(T)$, i.e. ${\rm div} (\boldsymbol x q) = (r-1+n)q$ for any $q\in\mathbb H_{r-1}(T)$, clearly we have ${\rm div} \mathbb P_r(T;\mathbb E^n) = \mathbb P_{r-1}(T) $. Hence the discrete inf-sup condition in one element always holds. The difficulty is the global version.

The key is the characterization of the range of the bubble functions.

The inclusion $ {\rm div}( \mathbb B_r({\rm div}, T)) \subseteq \mathbb P_{r-1}/\mathbb R$ is proved through integration by parts \(({\rm div} \boldsymbol v, p)_T = -( \boldsymbol v, \nabla p)_T = 0 \quad\forall~p\in \ker(\nabla ) = \mathbb R.\) If $ {\rm div}( \mathbb B_r({\rm div}, T)) \neq \mathbb P_{r-1}/\mathbb R$​, there exists a $p\in \mathbb P_{r-1}/\mathbb R$​ and $p\perp {\rm div}( \mathbb B_r({\rm div}, T))$​, which is equivalent to $\nabla p \perp \mathbb B_r({\rm div}, T)$​. Expand the vector $\nabla p$​ in the basis ${\boldsymbol n_i, i=1,\ldots, n}$​ as \(\nabla p = \sum\limits_{i=1}^n q_i {\boldsymbol n}_{i}\) with $q_i\in\mathbb P_{r-2}(T)$​​. Then set $\boldsymbol v_p = \sum\limits_{i=1}^n|\nabla\lambda_i| q_i \lambda_{0}\lambda_i \boldsymbol t_{i,0}\in \mathbb B_r({\rm div}, T)$​​, where $\boldsymbol t_{i,0}:=\texttt{v}_0-\texttt{v}_i$​​.

We have \((\nabla p, \boldsymbol v_p)_T = \sum_{i=1}^n \int_Tq_i^2 \lambda_{0}\lambda_i {\rm d}x = 0,\) which implies $q_i = 0$ for $i=1,2,\ldots, n$, i.e., $\nabla p = 0$ and $p = 0$ as $p\in \mathbb P_{r-1}/\mathbb R$.

---

To leave comments, please register a GitHub account and then you can sign in GitHub to write comments using Markdown and LaTeX.