Finite Element Complex
The epidemic has been going on for more than two years. During this period, one of my main research interests has been finite element complexes. Through a series of work with Xuehai Huang, as well as the discussion and communication with colleagues Hu Jun and Kaibo Hu, my understanding of conforming finite elements has really reached a higher level. I intend to write a series of posts to summarize my new understanding. Before going into the technical details, let’s take a look at the big picture.
Philosophically speaking, the understanding becomes clearer because there is a more systematic framework, which can put scattered various finite elements into a unified framework, such as the following finite element periodic table.
D. N. Arnold and A. Logg. Periodic Table of the Finite Elements, SIAM News, 47 (9), 2014.

From this point of view, our recent work has greatly expanded this element table to include almost all known conforming finite elements, while also constructing many more finite elements.
The extended area of the finite element periodic table is mainly the tensor finite elements. Existing finite element spaces usually approximates scalar or vector functions, and there are very few tensor finite element spaces, which is a bit stretched when solving partial differential equations (PDEs) containing tensors. Therefore, most of the applications of finite element methods are related to Laplacian equations, plus PDEs for vector functions such as Maxwell and Stokes equations. There is a large class of nonlinear PDEs in differential geometry that numerical solutions have not kept up with. One reason is the strong nonlinearity of these PDEs, and another is the absence of finite elements for tensors.
The construction of tensor finite elements can be put into the framework of finite element complexes. The main theoretical framework is the Bernstein-Gelfand-Gelfand (BGG) Construction recently established by Arnold and Kaibo, and the following is a 3-dimensional example. For details, refer to the paper
Arnold and K. Hu. Complexes from complexes. Found Comput Math. 2021.
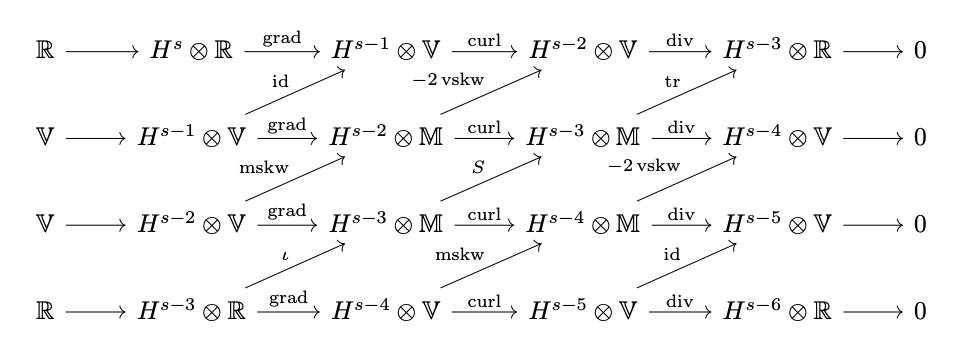
By tracing the diagram with cetain rules, one can get more complexes.
Ideally, finite element complexes can also be constructed in this way.
But it is too good to be true. The above diagram contains Sobolev spaces of infinite dimensions and functions are smooth enough. We call it continuous level. When considering the finite element spaces, the space is finite-dimensional and usually consists of polynomials which will be called discrete level. The polynomial space has great rigidity and will have many restrictions. In short, BGG cannot be directly applied to the discrete level.
Why? From continuous to discrete level, something must be lost. Consequently many structures in infinite-dimensional spaces cannot be maintained in finite-dimensional space. In other words, a finite-dimensional space has less room to move around freely.
Constructing a finite element is like dancing with shackles. It needs to fit the shape functions to the degrees of freedom exactly. Our work is already trying to unify the construction, but there’s still a lot to do with clever combinations. As we’ll see in a later series, even counting the dimensions of a finite element space is not that simple.
Technically speaking, combinatorics is used the most, and sort of algebraic topology. It will not use profound mathematical theory, but the construction process is also highly non-trivial. Let’s put it this way, My concern of my recent work is that the reviewers can’t understand it, or they are not patient to try to understand. One of the purposes of writing this series is to explain and explain from the perspective of ideas, so that our work can be better understood. There are strict rules for writing research articles, unlike blog posts where you can put more pictures and talk some non-rigorous but heuristic ‘proofs’. It’s impossible to include all calculation details in the paper, but trust us, every detail has been scrutinized. There might be typos, but there will be no essential mathematical errors for sure.
Our goal is the sea of stars. Constructing finite element spaces for tensors, ensuring the stability of numerical methods and the convergence of numerical solutions, is the first step in the Long March. In the next series of posts, I will take you slowly into the burgeoning research field of finite element complexes.

To leave comments, please register a GitHub account and then you can sign in GitHub to write comments using Markdown and LaTeX.
Comments