Professor of Mathematics at University of California, Irvine

less than 1 minute read

ABSTRACT. This chapter focuses on the geometric decomposition of the $C^m$-conforming finite elements on simplexes in arbitrary dimension constructed by Hu, Lin and Wu. The distance structure is introduced for the simplicial lattice to present a key non-overlapping decomposition of the simplicial lattice, in which each component will be used to determine the normal derivatives at each lower dimensional sub-simplex.

CONTENTS

  1. Distance and Derivative in Simplicial Lattice
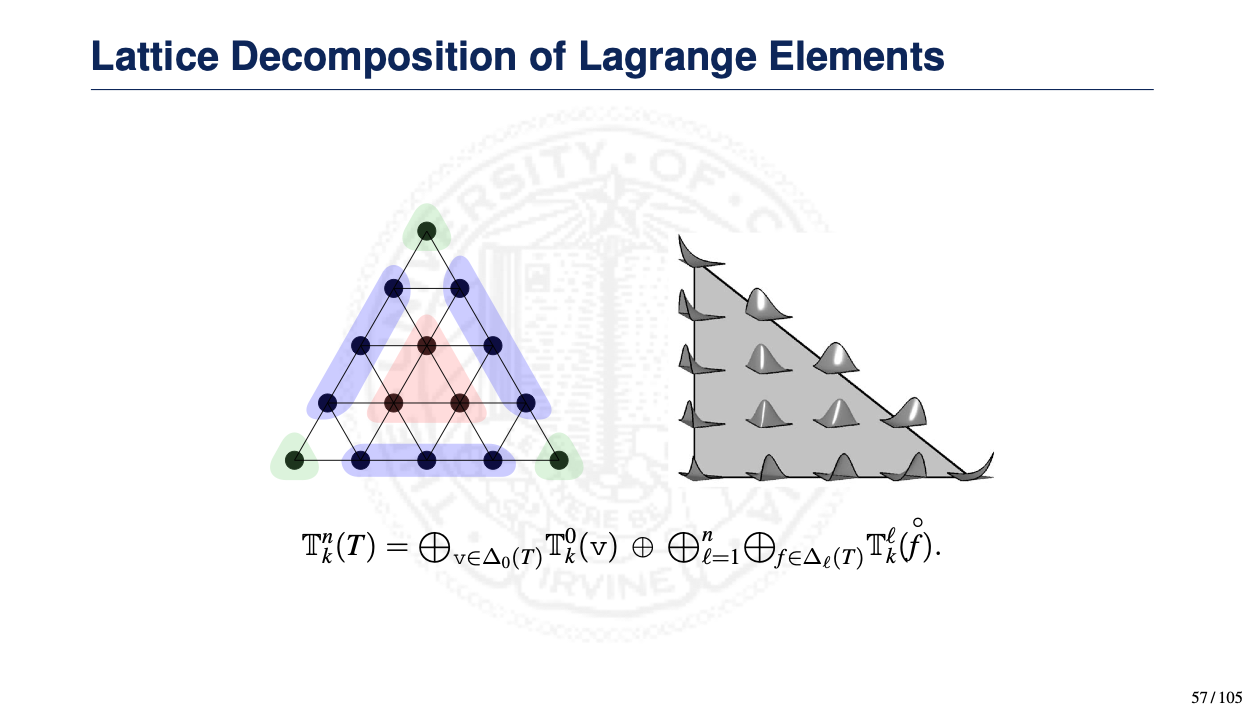
    • Simplicial lattices
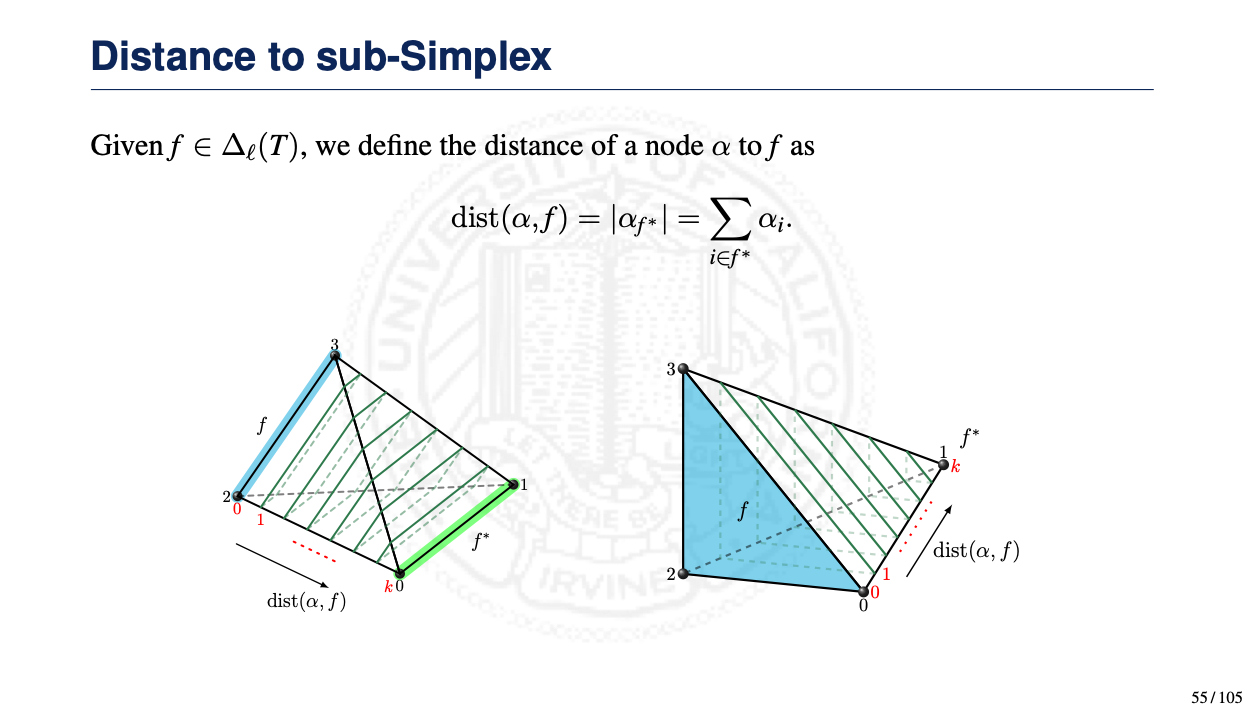
    • Distance
    • Derivative and distance
  2. Smooth Finite Elements in Two Dimensions
    • Examples in two dimensions
    • Derivatives at vertices
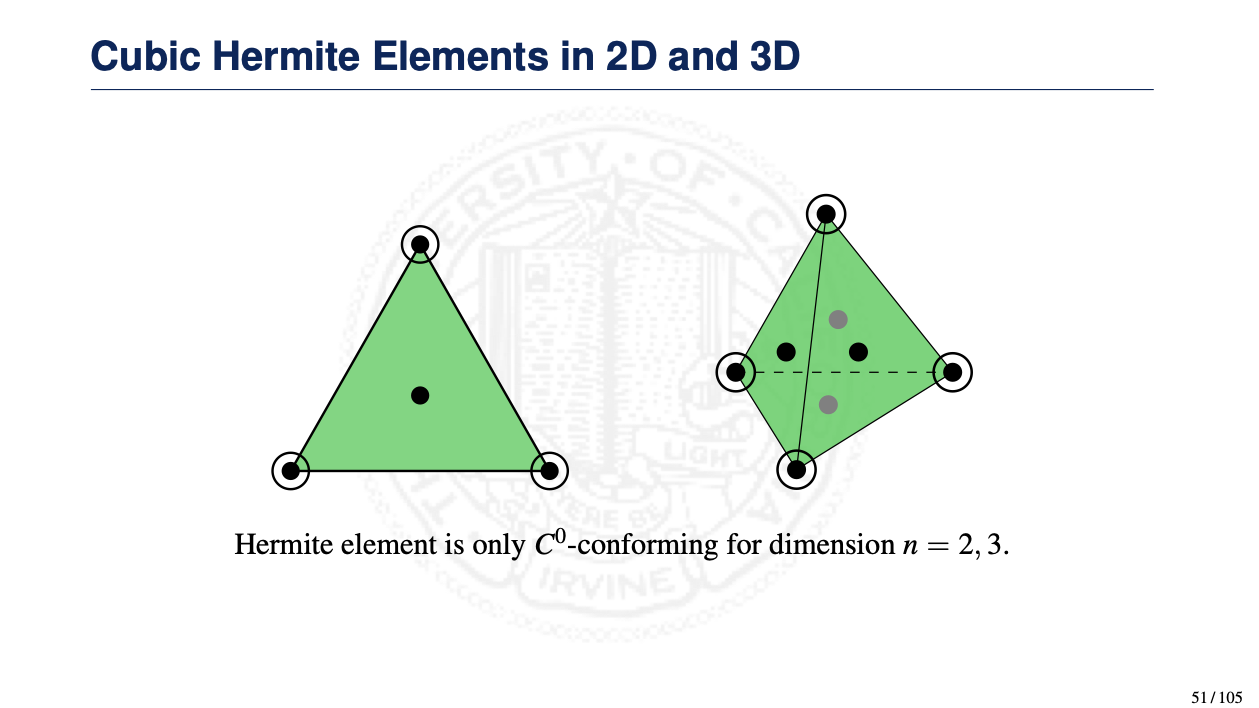
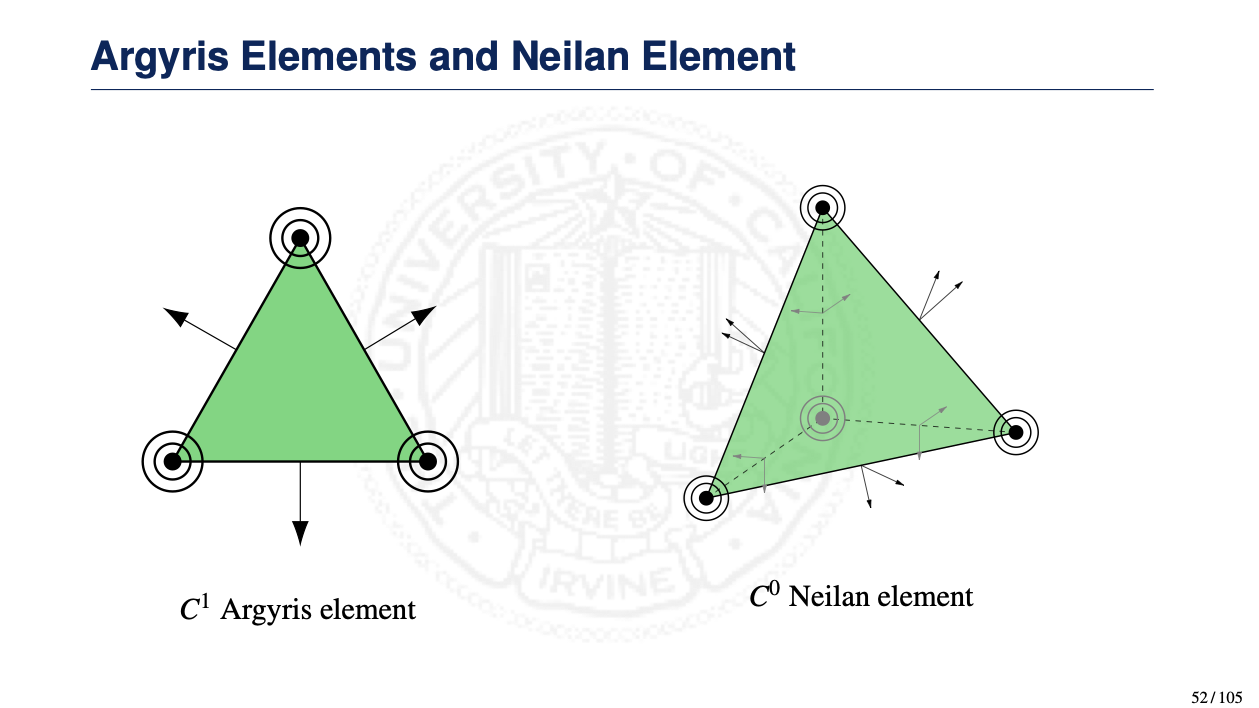
    • Hermite-type finite elements
    • Normal derivatives on edges
  3. Smooth Finite Elements in Arbitrary Dimensions
    • Decompositions of the simplicial lattice
    • Degrees of freedom
    • Smooth finite elements in arbitrary dimension

Chapter 3: Geometric Decomposition of Smooth Finite Elements

smoothFEM

smoothFEM 2

smoothFEM 3

Lagrangedec

smoothFEM 4

smoothFEM 5

smoothFEM 6

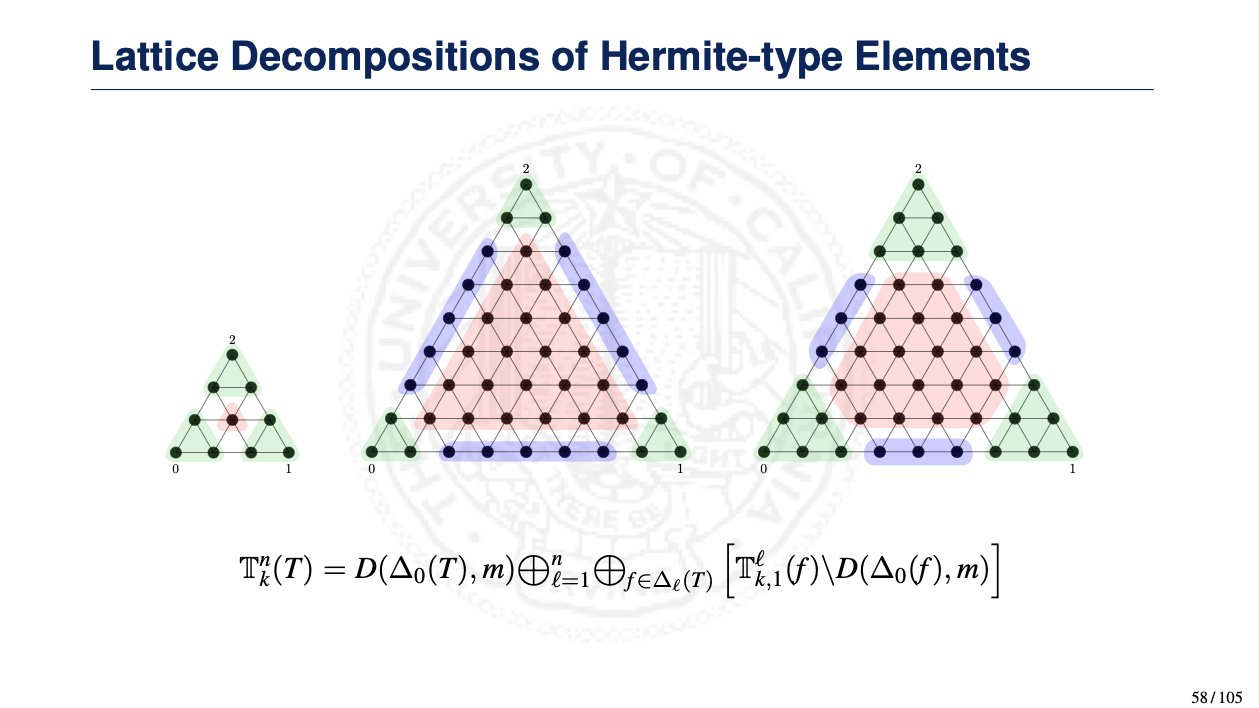
smoothFEM 7

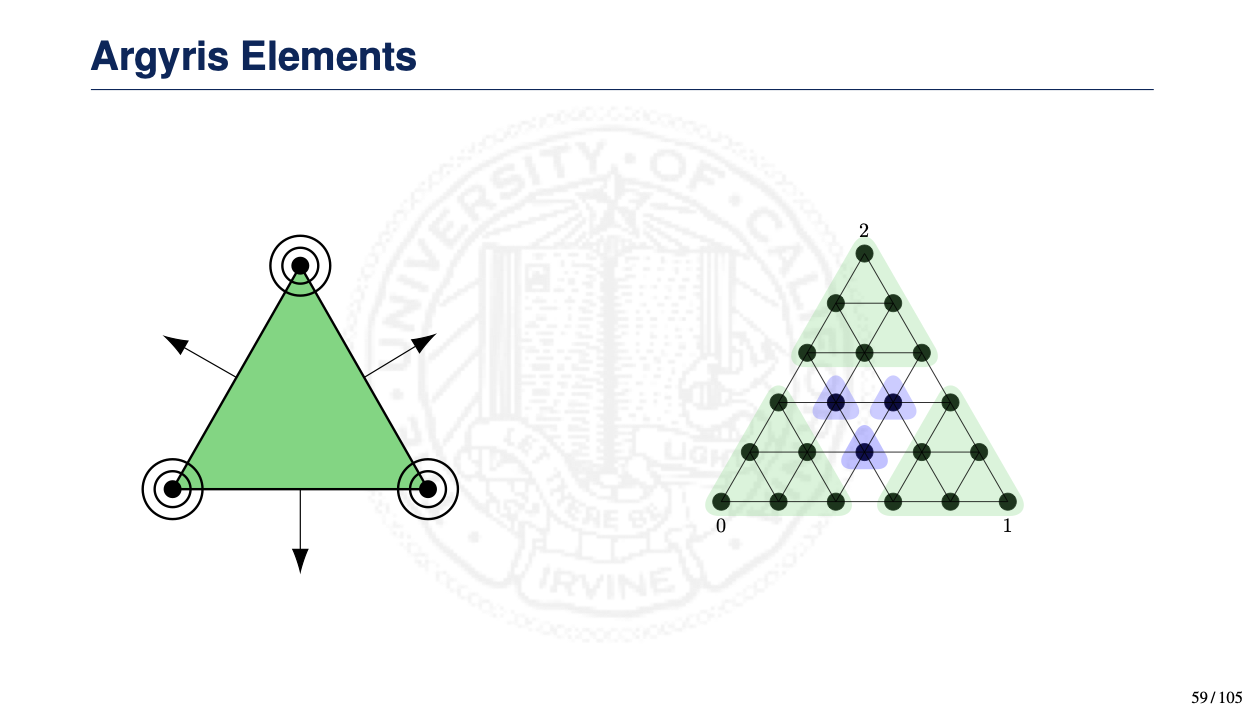
smoothFEM 8

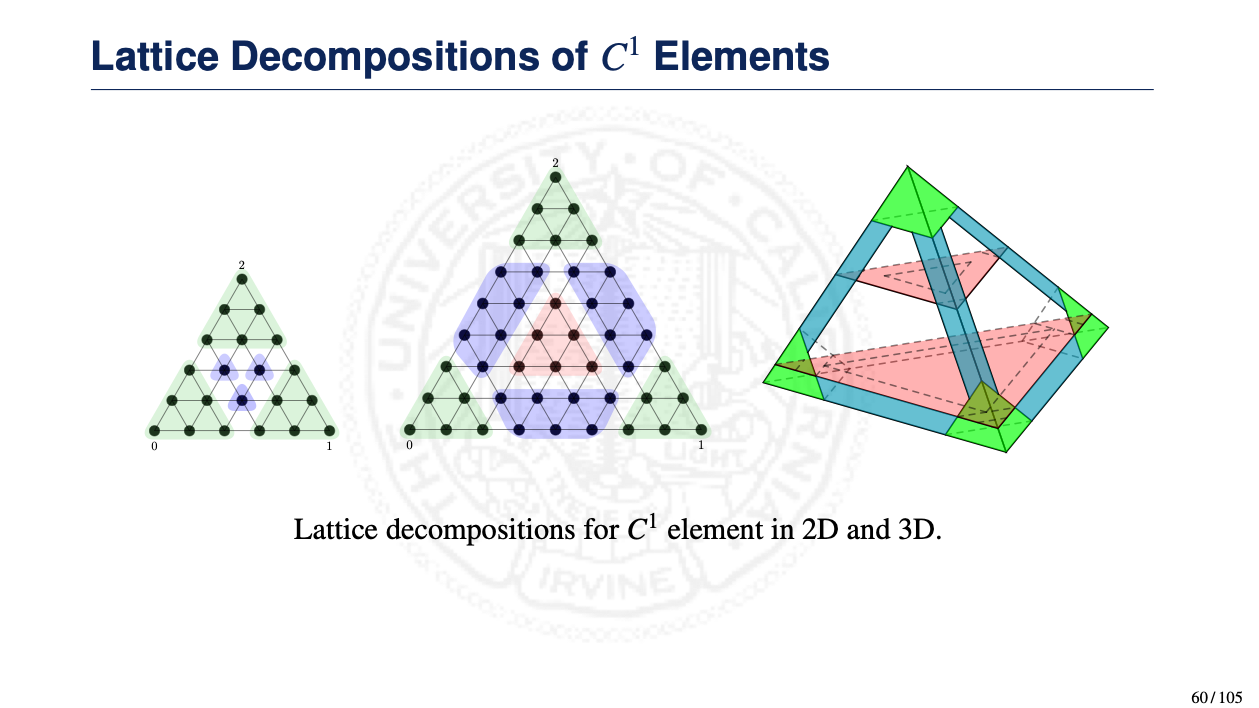
smoothFEM 9

smoothFEM 10

smoothFEM 11

smoothFEM 12

Chapter 3: Geometric Decomposition of Smooth Finite Elements

Comments

You May Also Enjoy

Chapter 1: Basics on Finite Elements

less than 1 minute read

ABSTRACT. This lecture notes covers the construction of finite element spaces, focusing on simplicial triangulations. Examples of finite elements, such as th...

Finite Element Complex

3 minute read

The epidemic has been going on for more than two years. During this period, one of my main research interests has been finite element complexes. Through a se...

Convex Set

8 minute read

We give an “inside" definition of convexity in which the order structure (not the linearity) plays an important role.