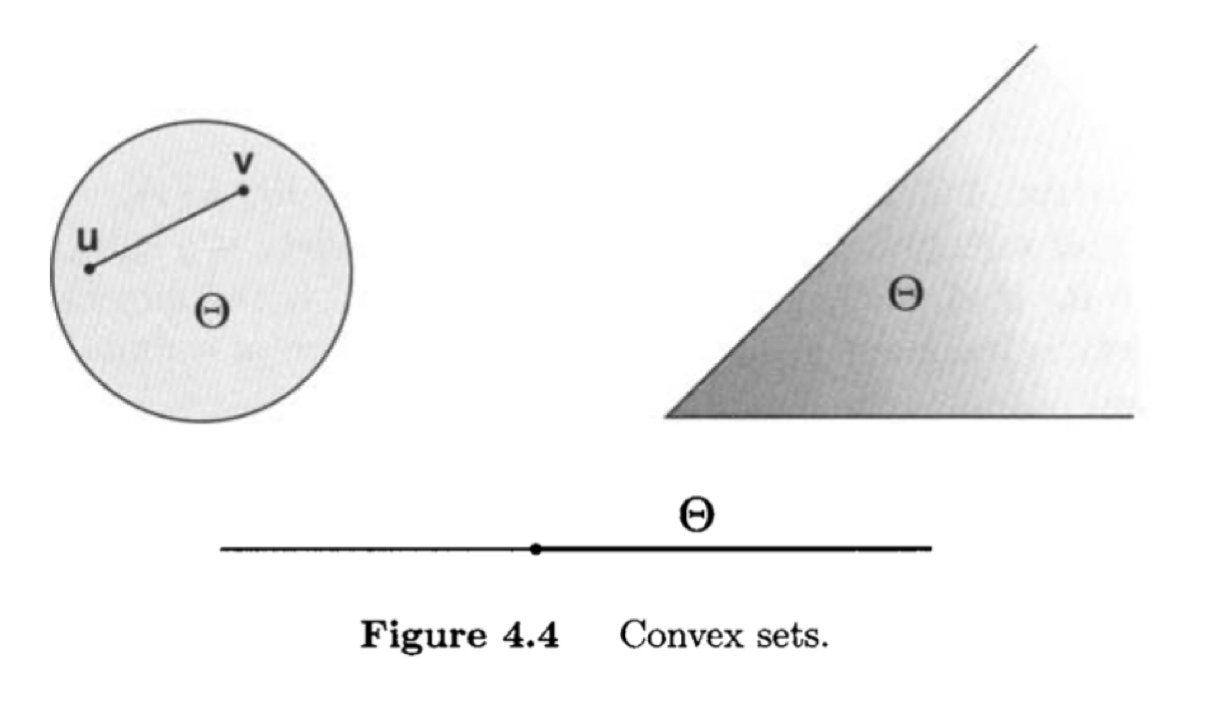
Convex Set

We give an “inside" definition of convexity in which the order structure (not the linearity) plays an important role.

Reference.

Functional analysis, calculus of variations and optimal control. F. Clarke. Springer. 2013.

Convex Sets

Definition

A subset $K$ of a linear space $V$ is convex if \(x,y\in K, \lambda \in (0,1) \longrightarrow (1- \lambda)x + \lambda y \in K.\) Recall for a linear subspace $S$, it requires $\alpha x + \beta y \in S$ for any $\alpha, \beta \in \mathbb R$. The convexity restricts the weight to $\alpha + \beta = 1, \alpha, \beta \geq 0$. Geometrically, convexity implies the line segment connecting $x$ and $y$ is inside the set while the linear subspace implies the plane spanned by vectors $x$ and $y$ is contained in the subspace. In particular, $0$ must be in a subspace while a convex set may not containing the origin.

The convexity is translation invariant. That is if $K$ is convex, so is $K + z :={x+ z: x\in K}$ for any $z\in V$ and $K+z \cong K$. The intrinsic property of a convex set is thus translation invariant. Depending on the context, assumption $0\in K$ or $0\notin K$ can be easily satisfied by translation.

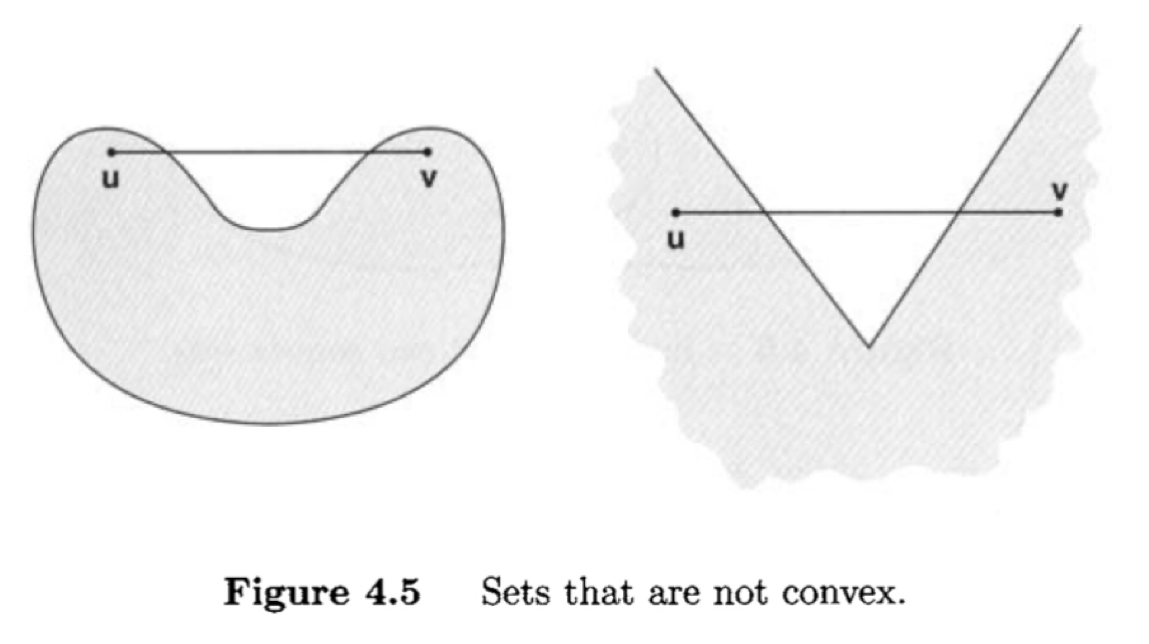
A convex set may not be closed, e.g., an open ball. A convex set may not be bounded. An example is a convex cone $K$ which is defined as if $x\in K$, then $\lambda x\in K$ for all $\lambda \geq 0$. On the other hand, a cone may not be convex as by definition it contains the whole ray $\lambda x$ for all $\lambda \in \mathbb R$. A convex set may not contain an interior point, e.g., a line segment in $\mathbb R^n, n> 1$.

Minkowski Functional

In the philosophy of Descartes, we introduce an algebraic tool to study the geometry of convex sets.

Definition 1. Let $K$ be a set in a normed vector space $V$. The Minkowski functional or gauge function of $K$ is a functional $p: V \rightarrow \mathbb{R}$, defined by \(p(v)=\inf \{\lambda>0, v \in \lambda K\}.\)

By convention, $\inf\varnothing = +\infty$. To be real valued, we assume $0\in \stackrel{\circ}{K}$. Then $p$ has value in $[0,\infty)$.

Minkowski functional allow one to “translate" some geometry properties of a subset into algebraic properties of a function. For example, \(\label{eq:Kp} \stackrel{\circ}{K} = \{x: p(x) < 1\}, \quad \overline{K} = \{x: p(x) \leq 1\}.\) For $x\notin K$, $p(x)$ is the factor by which the set $K$ must be dilated in order to include the point $x$. The Minkowski functional of the unit ball $B_{1}(0)$ is the norm $|\cdot|$.

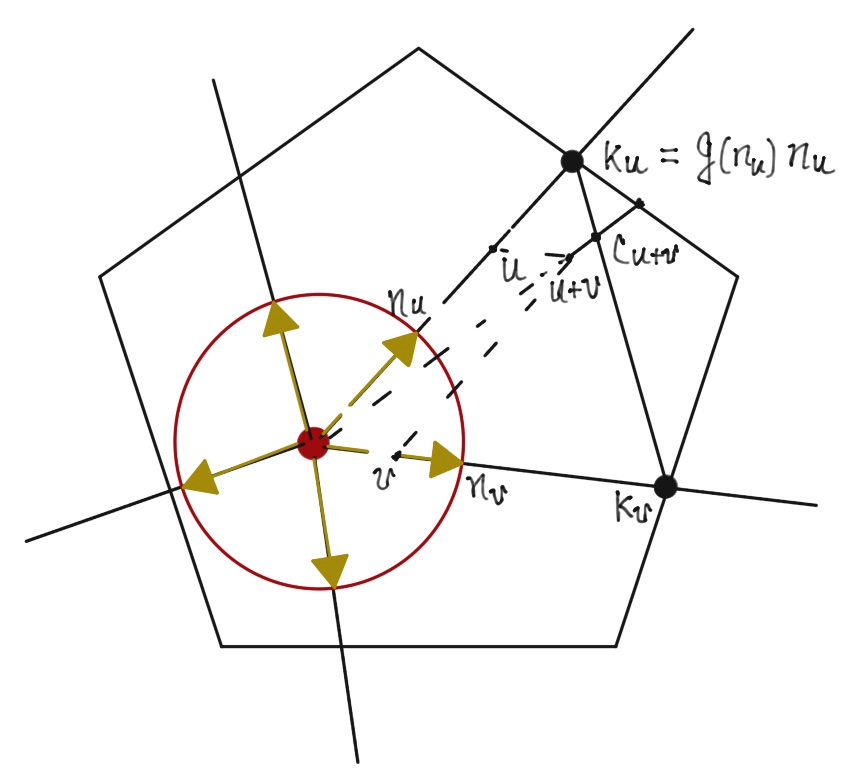
As convexity is translation invariant, we can set an element of $K$ as the origin and define a function on the unit sphere \(g: S_1(0)\to \mathbb R_{+}\quad g(n) = \sup \{\mu > 0, \mu n\in K\}.\) It can be thought of as the diameter of $K$ in the direction $n$. If $K$ is unbounded in the direction $n$, then $g(n) = +\infty$. Let $n_v = v/|v|$ be the direction vector of $v$. Then we have the relation \(p(v) = \frac{\|v \|}{g(n_v)}, \quad v = p(v) g(n_v)n_v. \label{eq:pg}\) The point $k(v) :=g(n_v)n_v\in \bar K$ is the furtherest point in $\bar K$ in the direction $n_v$ and $p(v)$ is the ratio $|v|/|k(v)|$. The identity $\eqref{eq:pg}$ generalizes the relation of Minkowski functional and the norm. When $K$ is the unit ball $B_{1}(0)$, $p(\cdot)$ is the norm $|\cdot|$.

The convexity property is translated to the algebraic property: the Minkowski functional is sub-linear.

Recall that A real-valued function $p: X\to \mathbb R$ is called a sublinear function or sometimes called a quasi-seminorm if it has these two properties:

• Positive homogeneity/Nonnegative homogeneity: $p(rx)=rp(x)$ for all real $r\geq 0,x \in X$.
• Subadditivity/Triangle inequality: $p(x+y)\leq p(x)+p(y)$ for all $x,y\in X$

Lemma 2. Let $K$ be a nonempty convex set in a normed vector space $V$ such that $0 \in \stackrel{\circ}{K}$. Then $p(v)=\inf {\lambda>0, v\in \lambda K}$ is sub-additive and positive homogeneous.

Proof. The positive homogeneity follows from $p(v) = |v |/g(n_v)$ as $g$ depends only on direction. No convexity is required.

The convexity will imply $p$ is sub-additive. Consider the case $K$ is bounded and closed. Then $n_u g(n_u)$ is the intersection of the ray and $\partial K$ and \(u = n_u g(n_u) p(u) = p(u) k(u), k_u\in K.\) Then \(u+ v = p(u)k(u) + p(v) k(v) = (p(u) + p(v)) c_{u+v}, \notag\) where the element \(c_{u+v}:=\left ( \frac{p(u)}{p(u) + p(v)} k(u) + \frac{p(v)}{p(u) + p(v)} k(v)\right )\in K \notag\) and its norm is bounded by $g(n_{u+v})$ by definition. Take norm both sides to get \(p(u) + p(v) = \frac{\| u + v\|}{\|c_{u+v}\|} \geq \frac{\| u + v\|}{\|g(n_{u+v})\|} = p(u+v). \notag\)

Minkowski Sum/Difference

The Minkowski sum/difference of two sets $A$ and $B$ in a vector space $V$ is \(A+B:=\{ a+ b \mid a\in A, b\in B\},\\ A-B:=\{ a - b \mid a\in A, b\in B\}.\) Recall that $A+b$ is a translation of $A$. Then $A+B$ consists of copies of $A$ with center moving around the points in $B$. Think about the clone stamp tool in Photoshop.

Examples.

1. Sum of one vertical line and a horizontal line is a square.

2. Sum of two disks are a larger disk.

   

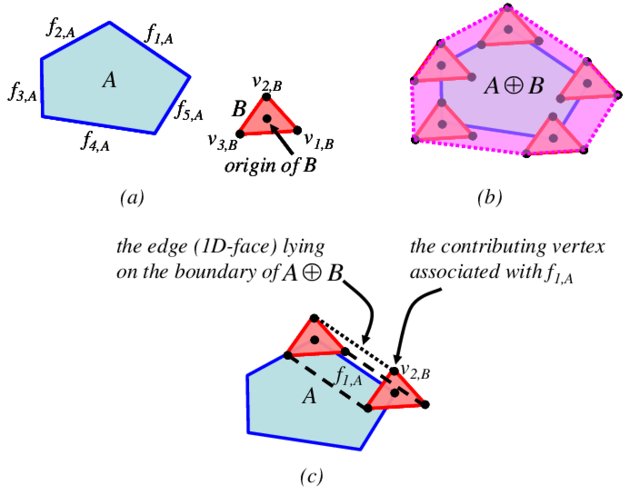
If $A$ and $B$ are convex subsets of a vector space $V$, then $A+B$ and $A-B$ are convex.

Separation of Convex Sets

Finite dimensional Hilbert spaces

We start from convex sets in $\mathbb R^n$ for which we can use the inner product structure.

Lemma 3. Let $K$ be a nonempty closed convex set in $\mathbb R^n$. Let $v\notin K$ be a point not in $K$. Then there exists a unique solution to the optimization problem \(\label{eq:dist} {\rm dist} (v, K) := \inf_{x\in K} \| v - x \|.\) And the solution $x^$ *is defined as the projection of $v$ to $K$ and denoted by $P_K(v) = x^*$.

The existence of the minimizer will depend on the completeness of $\mathbb R^n$ and the convexity implies the uniqueness. Then use the vector $n = v - P_K v$ as a normal vector and set $c = (n, P_Kv)$ to define a hyperplane separating the point $v$ with $K$.

Lemma 4. Let $K$ be a nonempty, closed, and convex subset of $\mathbb R^n$. Let $v\not\in K$. Then $K$ and $v$ is separated by the hyperplane $\mathcal H(n,c)={x\in \mathbb R^n: (n, x) = c}$ with $n = v- P_Kv$ and $c = (n, P_Kv)$ in the sense that \((p, x) < (p, v) \quad \forall x\in \stackrel{\circ}{K}. \notag\)

Hahn-Banach separation theorem

When move to a normed vector space $X$, there is no inner product and no compactnesss assumed. The tool to use is the Hahn-Banach Theorem and the sub-linear functional to compare is the Minkowski functional.

We first use the duality pair to generalize the definition of hyperplanes: \(\mathcal H(f,c) := \{x \in X:\langle f, x\rangle=c\},\) where $0 \neq f \in X^{*}$ and $c$ is a scalar, is referred to as a hyperplane. Halfspaces can be defined by using $\leq$ or $\geq$. Roughly speaking, we speak of two sets $K_{1}$ and $K_{2}$ as being separated if there is a hyperplane such that $K_{1}$ is contained in one of the associated halfspaces, and $K_{2}$ in the other.

Lemma 5. Let $K$ be open convex set containing $0$ and there exists $v\not\in X$. Then there exists a hyperplane $\mathcal H(f,c)$ separating $v$ and $K$ \(\langle f, x\rangle < \langle f, v\rangle \quad \forall x\in K.\) Proof. Like the $\mathbb R^n$ case, we are going to use $\langle f, x \rangle$ to change set to interval in $\mathbb R$. The extension in Hilbert space is naturally done by the inner product and the extension in a normed vector space will be achieved by Hahn-Bahn theorem.

Take the 1-D subspace $S = { t v: t\in \mathbb R}$ and define $f(tv) = t$. The sub-linear function $p$ is the Minkowski functional $p$ of $K$. As $v\not\in K$, $p(v)\geq 1$. Verification $f(x) \leq p(x)$ for all $x\in S$ is straightforward. Then we can extend and still denote by $f\in X’$.

Then $\langle f, x\rangle \leq p(x)< 1 = \langle f, v\rangle$ for $x\in K$. The last inequality is strict as $K$ is open. ◻

Theorem 6 (Hahn-Banach separation). Let $K_{1}$ and $K_{2}$ be nonempty, disjoint convex subsets of the normed vector space $X$. They can be separated in the two following cases:

1. If $K_{1}$ is open, there exist $f \in X’$ and $\gamma \in \mathbb{R}$ such that \(\langle f, x\rangle<\gamma \leqslant\langle f, y\rangle \quad \forall x \in K_{1}, y \in K_{2}. \notag\)

2. If $K_{1}$ is compact and $K_{2}$ is closed, there exist $p \in X’$ and $\gamma_{1}, \gamma_{2} \in \mathbb{R}$ such that \(\langle f, x\rangle<\gamma_{1}<\gamma_{2}<\langle f, y\rangle \quad \forall x \in K_{1}, y \in K_{2} .\) The second type of separation above is called strict.

Proof. (1) Pick up $x_1\in K_1$ and $x_2\in K_2$ and set $v = x_2 - x_1$. Let $K = K_1 - K_2 + v$. Then $K$ is an open convex set containing $0$ and $v\in K$ since $K_1\cap K_2 = \varnothing$. We apply Lemma 5 to find $f$ separating $v$ and $K$.

For arbitrary $x\in K_1, y\in K_2$. The point $x - y + v\in K$. We have \(\langle f, x\rangle - \langle f, y\rangle + \langle f, v\rangle = \langle f, x-y +v \rangle < \langle f, v\rangle, \notag\) which implies \(\langle f, x\rangle<\langle f, y\rangle \quad \forall x \in K_{1}, y \in K_{2}. \notag\) Then chose $\gamma = \sup f(K_1)$ to obtain the desired conclusion.

(2) We can extend $K_1$ slightly as $K_{1+\epsilon}:= K_1 + \stackrel{\circ}B_{\epsilon}(0)$ which is open and convex and still disjoint with $K_2$. The compactness of $K_1$ is used to find finite covering using small balls to define such an extension. $K_2$ is closed means such ball exists as $K_2^c$ is open. Then apply (1). Now the inequality \(\max f(K_1) < \sup f( K_{1+\epsilon}) \leq \inf f(K_2) \notag\) implies the existence of $\gamma_1, \gamma_2$ as required. ◻