Coarsen in Two Dimensions

We describe the coarsening algorithm implemented in coarsen.m for two dimensional bisection grids. We assume when bisecting a triangle, the left child is stored in a prori of the right child. More details can be found in the paper,

@article{ChenZhang2010,
  title={A coarsening algorithm on adaptive grids by newest vertex bisection and its applications},
  author={Chen, Long and Zhang, Chensong},
  journal={Journal of Computational Mathematics},
  pages={767--789},
  year={2010},
  publisher={JSTOR}
}

Compatible Bisection

Every bisection grids can be obtained from an initial grid with a sequence of compatible bisections. In two dimensions, there are two types of compatible bisections.

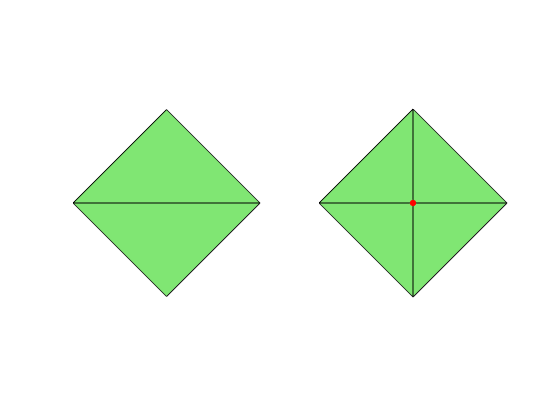
  • Case 1: A pair of triangles are divided into four triangles by adding the middle point their common edge.
node = [1,0; 0,1; -1,0; 0,-1];
elem = [2 3 1; 4 1 3];
figure(1); 
subplot(1,2,1); showmesh(node,elem);
[node,elem] = bisect(node,elem,[1 2]);
subplot(1,2,2); showmesh(node,elem); 
findnode(node,5,'noindex');

png

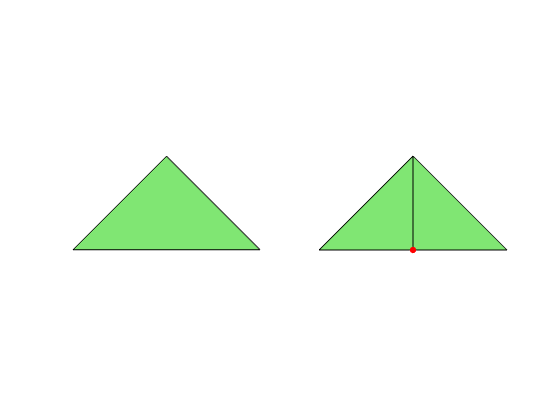
  • Case 2: A triangle containing a boundary edge is divided into two triangles by adding the middle point the boundary edge.

The nodes added by compatible bisections are called good-to-carsen nodes or simpley good nodes.

elem = [2 3 1];
subplot(1,2,1); showmesh(node,elem);
[node,elem] = bisect(node,elem,1);
subplot(1,2,2); showmesh(node,elem); 
findnode(node,5,'noindex');

png

Coarsening Procedure

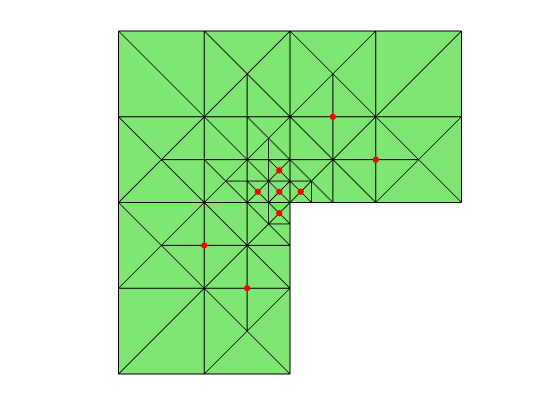
Our coarsening algorithm consists of finding good nodes and removing them. The coarsening procedure is illustrated by the following figures.

load Lshapemesh
figure
for k = 1:3
    subplot(1,3,k); showmesh(node,elem);
    [node,elem] = coarsen(node,elem,'all');
end

png

Step 1 – Find Good Nodes

We use the following characterization to find a good node p

  • The valence of p is 4 (interior node) or 2 (boundary node).
  • It is the newest vertex of all triangles in its nodal star.
load Lshapemesh
N = size(node,1); 
NT = size(elem,1);
valence = accumarray(elem(:),ones(3*NT,1),[N 1]);
valenceNew = accumarray(elem(:,1),ones(NT,1), [N 1]); % for newest vertex only
allNodes = (1:N)';
intGoodNode = allNodes((valence==valenceNew) & (valence==4));
bdGoodNode = allNodes((valence==valenceNew) & (valence==2));
figure(2); showmesh(node,elem);
findnode(node,intGoodNode,'noindex');
findnode(node,bdGoodNode,'noindex');

png

Step 2 – Remove Good Nodes

The star of good nodes are found using the incides matrix between triangles and vertices.

t2v = sparse([1:NT,1:NT,1:NT], elem(1:NT,:), 1, NT, N);
[ii,jj] = find(t2v(:,intGoodNode));
nodeStar = reshape(ii,4,length(intGoodNode));

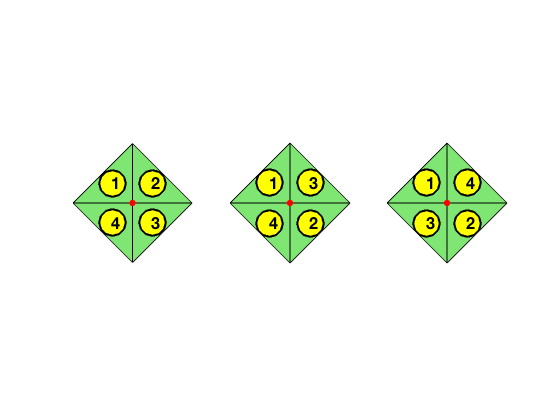
For interior good nodes, there are 3 configurations of 4 triangles in the star of a good node showing the following figures. Other combinations are ruled out by our ordering assumption: the left child is stored in a prori of the right child. Therefe nodeStar(:,1) is always in L type and nodeStar(:,4) is in R type. Here the oritentation is respect the direction from the new added vertex to the opposite vertex in each triangle.

figure(1);
node1 = [1,0; 0,1; -1,0; 0,-1; 0,0];
elem1 = [5 3 2; 5 1 2; 5 4 1; 5 3 4];
subplot(1,3,1); showmesh(node1,elem1); findelem(node1,elem1);
findnode(node1,5,'noindex');
elem1 = [5 3 2; 5 4 1; 5 1 2; 5 3 4];
subplot(1,3,2); showmesh(node1,elem1); findelem(node1,elem1);
findnode(node1,5,'noindex');
elem1 = [5 3 2; 5 4 1; 5 3 4; 5 1 2];
subplot(1,3,3); showmesh(node1,elem1); findelem(node1,elem1);
findnode(node1,5,'noindex')

png

% We switch the local indices of nodal star to the first case. 
ix = (elem(nodeStar(1,:),3) == elem(nodeStar(4,:),2));
iy = (elem(nodeStar(2,:),2) == elem(nodeStar(3,:),3));
% nodeStar(:,ix & iy)  = nodeStar([1 2 3 4],ix & iy);
nodeStar(:,ix & ~iy) = nodeStar([1 3 2 4],ix & ~iy);
nodeStar(:,~ix & iy) = nodeStar([1 4 2 3],~ix & iy);
% nodeStar(:,~ix & ~iy)= nodeStar([1 4 3 2],~ix & ~iy);
%%
% We label the local indices of nodes in the star in the following figure.
figure(2)
node1 = [0,0; -1,0; 1,0; 0,1; 0,-1];
elem1 = [1 4 2; 1 3 4; 1 2 5; 1 5 3];
showmesh(node1,elem1); findelem(node1,elem1); findnode(node1);

png

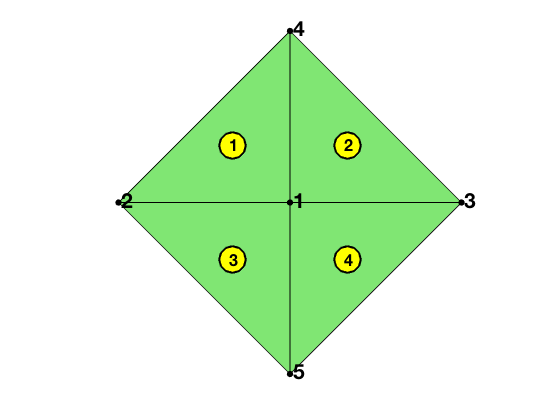
Then t1 and t2 are merged to a big triangle and stored in t1 and similarly t3 and t4 are merged together and stored in t3. Elements t2 and t4 will be removed later on.

t1 = nodeStar(1,:); 
t2 = nodeStar(2,:); 
t3 = nodeStar(3,:);
t4 = nodeStar(4,:);
% p1 = elem(t1,1); 
p2 = elem(t1,3); 
p3 = elem(t2,2); 
p4 = elem(t1,2); 
p5 = elem(t3,2);
elem(t1,:) = [p4 p2 p3]; 
elem(t2,1) = 0;
elem(t3,:) = [p5 p3 p2]; 
elem(t4,1) = 0;

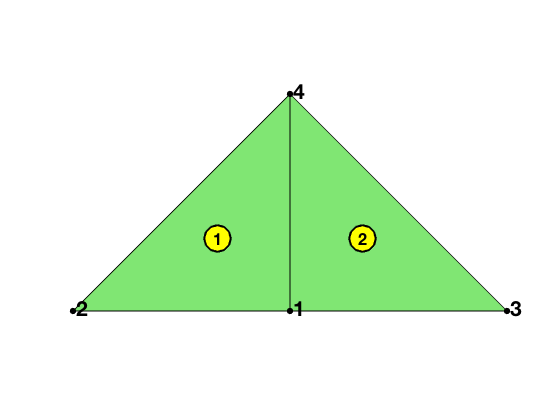
For boundary good nodes, there is only one case.

figure(2)
node1 = [0,0; -1,0; 1,0; 0,1];
elem1 = [1 4 2; 1 3 4];
showmesh(node1,elem1); findelem(node1,elem1); findnode(node1);
[ii,jj] = find(t2v(:,bdGoodNode));
nodeStar = reshape(ii,2,length(bdGoodNode));
t1 = nodeStar(1,:); 
t2 = nodeStar(2,:);
p1 = elem(t1,1); 
p2 = elem(t1,3); 
p3 = elem(t2,2); 
p4 = elem(t1,2);
elem(t1,:) = [p4 p2 p3]; 
elem(t2,1) = 0;

png

Clean and Shift Node and Elem Matrices

The empty rows in node and elem matrices should be released for the efficient usage of memory.

elem((elem(:,1) == 0),:) = [];
isGoodNode = false(N,1);
isGoodNode(intGoodNode) = true;
isGoodNode(bdGoodNode) = true;
node(isGoodNode,:) = [];

Note that the indices of nodes in the coarsened mesh is changed while elem still use the indices in the fine mesh. We build the indices map between the fine grid to the coarse grid. For example, indexMap(10) = 6 means the 10-th node in the fine grid is now the 6-th node in the coarse one.

indexMap = zeros(N,1);
indexMap(~isGoodNode)= 1:size(node,1);
elem = indexMap(elem);

In the application to adaptive finite element methods, we will remove good-to-coraen nodes whose star are marked for coarsening.

In the application to multigrid methods, we will record all neighboring nodes in the nodal star of good nodes; see the function: uniformcoarsen.

The 3-D coarsening algorithm is slightly complicated than the 2-D case.

Additional data structure

  • bdFlag stores information on boundary conditions. It is updated as

bdFlag(t1,:) = [bdFlag(t1,2) bdFlag(t2,1) bdFlag(t1,1)]; bdFlag(t3,:) = [bdFlag(t3,2) bdFlag(t4,1) bdFlag(t3,1)]; bdFlag(t5,:) = [bdFlag(t5,2) bdFlag(t6,1) bdFlag(t5,1)]; bdFlag((elem(:,1) == 0),:) = [];

  • tree(:,1:3) stores the binary tree of the coarsening. tree(:,1) is the index of parent element in the coarsened mesh and tree(:,2:3) are two children indices in the original mesh.

tree = zeros(NTdead,3,'uint32'); tree(1:NTdead,1) = [t1'; t3'; t5(idx)']; tree(1:NTdead,2) = [t1'; t3'; t5(idx)']; tree(1:NTdead,3) = [t2'; t4'; t6(idx)'];

Comments