Project: Linear Finite Element Methods
The purpose of this project is to implement the finite element method for solving the Poisson equation in a general polygonal domain using the piecewise linear finite element.
Step 1: Download and install iFEM
- Clone or download the zip file of iFEM from GitHub.
- If a zip folder is dowloaded, unzip the file to where you like.
- In MATLAB, go to the iFEM folder .
- Run
setpath.m.
Step 2: Mesh
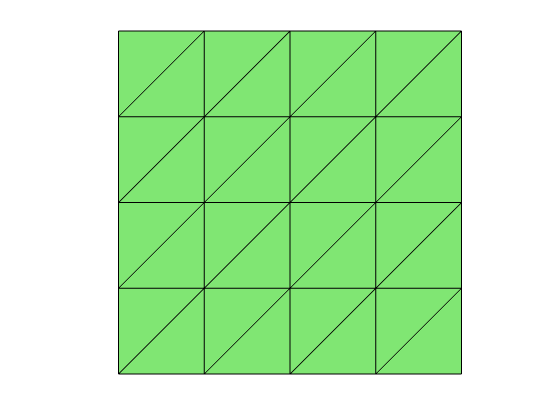
% Generate mesh for the unit square
[node,elem] = squaremesh([0,1,0,1],0.25);
showmesh(node,elem);
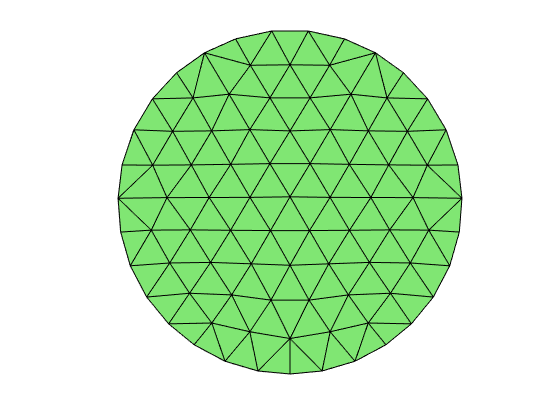
% Generate mesh for the unit disk
[node,elem] = circlemesh(0,0,1,0.2);
showmesh(node,elem);
- Min quality 0.7570 - Mean quality 0.9696 - Uniformity 4.34%
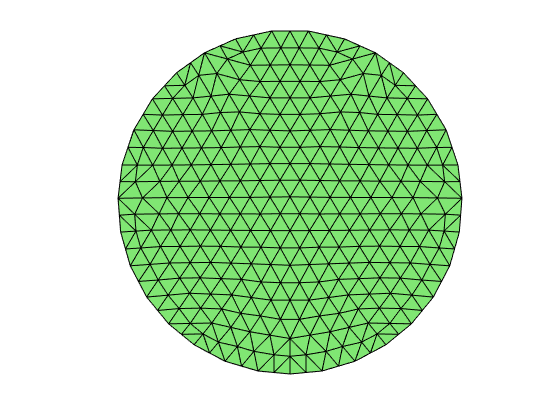
% Uniformly refine it to get a finer mesh
[node,elem] = uniformrefine(node,elem);
showmesh(node,elem);
Step 3: Assembling the matrix
Compare three ways of assembling the stiffness matrix discussed in Progamming of Finite Element Methods.
Record the time by
tic; assemblingstandard; toc;
tic; assemblingsparse; toc;
tic; assembling; toc;
Compare the computational time for different N by applying the uniform refinement of the initial mesh several times. Try to test the assembling until N > 5*1e^4.
Step 4: Right hand side
Using three points quadrature (i.e. 3 middle points of a triangle) to compute the right hand side vector.
Step 5: Boundary conditions
- Use
findboundary.mto get all boundary nodes and edges - Code pure Dirichlet boundary condition $u = g_D$
- Code pure Neumann boundary condition $\nabla u\cdot n = g_N$
- (optional) Code Robin boundary condition $u + d\nabla u\cdot n = g_R$
Step 6: Verify convergence
-
Choose a smooth solution, say $u = \sin(2\pi x)\cos(2\pi y)$, calculate the right hand side $f$ and boundary conditions for the unit square.
-
Use your subroutine to get an approximation and use
showresultto plot the mesh and the solution. -
Use
uniformrefineto refine the mesh and compute a sequence of solutions. -
Compute the error in $H^1$-norm and $L^2$-norm using
getH1errorandgetL2error. -
Use the stiffness matrix to compute the error $|\nabla(u_I - u_h)|$, where $u_I$ is the nodal interpolation.
-
Use
showratehto plot the rate of convergence of these error. -
Test both Dirichlet and Neumann problems.
Step 7: A challenging problem
Code your subroutine in a general way such that you can solve the Poisson equation on a different mesh by changing the input arguments.
After you get the desireable results for the unit square, try to solve $-\Delta u = 1$ with constant Neumann boundary conditions on the unit disk. The exact solution can be found using a separation of variable in the polar coordinate.
Comments