Mesh Smoothing and Optimization

Improve geometric mesh quality

The function

[node,elem] = optmesh(node,elem)

will optimize the shape regularity of triangles in the input mesh (node,elem) and outputs a better mesh (node,elem). Note that the connectivity, i.e., elem might be changed. Use

node = meshsmoothing(node,elem)

to move nodes only.

After showing an example, we shall explain algorithms implemented in optmesh.m.

load airfoilperturbmesh
figure(1); subplot(1,2,1); 
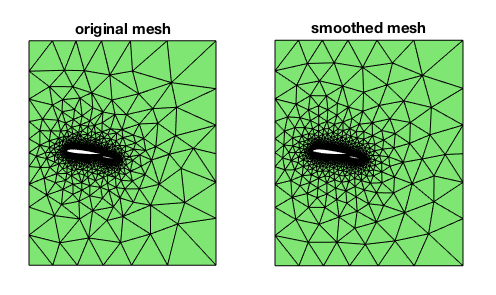
showmesh(node,elem); title('original mesh');
figure(2); subplot(1,2,1); 
showmeshquality(node,elem); axis([0 1 0 2700]);
[node,elem] = optmesh(node,elem);
figure(1); subplot(1,2,2); 
showmesh(node,elem); title('smoothed mesh');
figure(2); subplot(1,2,2); 
showmeshquality(node,elem); axis([0 1 0 2700]);

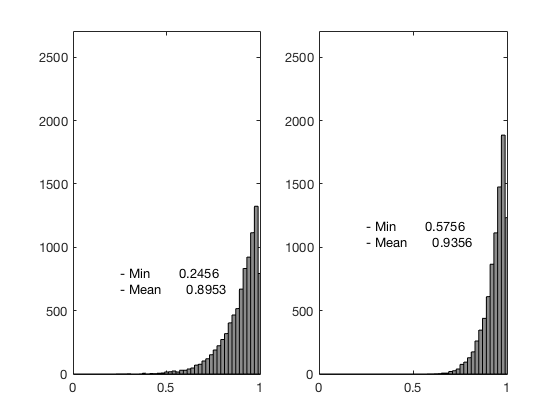
 - Min quality 0.2456 - Mean quality 0.8953 
Mesh quality before optimization 
 - Min quality 0.2456 - Mean quality 0.8953 
Mesh quality after optimization 
 - Min quality 0.5756 - Mean quality 0.9356 
 - Min quality 0.5756 - Mean quality 0.9356

png

png

ODT-based mesh smoothing

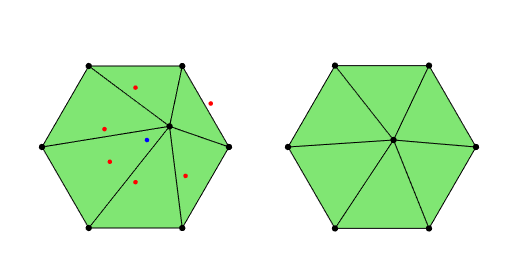
In the function meshsmoothing, we move one node at a time inside its patch, which consists of all triangles surrounding this node, such that the interpolation error to the quadratic function $z=x^2+y^2$ is minimized. The function meshsmoothing will keep the topology of the input mesh, i.e., the node index and connectivity of nodes are unchanged.

In the simplest case, the scheme is to move the node to the average of circumenters of triangles in the local patch. Details can be found in my research webpage ODT mesh.

theta = [-2*pi/3 -pi/3 0 pi/3 2*pi/3 pi]';
node = [cos(theta), sin(theta)];
node(end+1,:) = 0;
elem = delaunayn(node);
node(end,:) = rand(1,2)*0.4;
figure(3); subplot(1,2,1);
showmesh(node,elem); findnode(node,'all','noindex');
c = circumcenter(node,elem);
hold on; plot(c(:,1),c(:,2),'r.','MarkerSize',16)
node(end,:) = mean(c);
plot(node(end,1),node(end,2),'b.','MarkerSize',16)
figure(3); subplot(1,2,2);
showmesh(node,elem); findnode(node,'all','noindex');

png

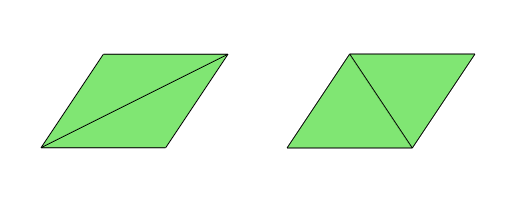
Edge swapping

Edge swapping is used to further improve the mesh quality. elem = edgeswap(node,elem) swap diagonals of a convex quadlateral formed by two triangles of the mesh (node,elem) such that the summation of opposite angles are less than or equal to 180 degree, i.e., it is locally Delaunay.

Since the connectivity may be changed, some elementwise quantity, e.g., the material property, if any, should be updated accordingly.

node = [0,0; 1,0; 0.5, 0.75; 1.5, 0.75];
elem = [1 2 4; 4 3 1];
subplot(1,2,1); showmesh(node,elem);
elem = edgeswap(node,elem);
subplot(1,2,2); showmesh(node,elem);

png

Reference

  • L. Chen and J. Xu. Optimal Delaunay Triangulations. Journal of Computational Mathematics. 299–308, 2004.
@article{ChenXu2004,
  title={Optimal delaunay triangulations},
  author={Chen, Long and Xu, Jinchao},
  journal={Journal of Computational Mathematics},
  pages={299--308},
  year={2004}
}

@inproceedings{chen2004mesh,
  title={Mesh Smoothing Schemes Based on Optimal Delaunay Triangulations.},
  author={Chen, Long},
  booktitle={IMR},
  pages={109--120},
  year={2004}
}

Comments