Uniform Red Refinement in 3D
It subdivides each tetrahedron in a triangulation into eight
subtetrahedra of equal volume. The ordering of sub-tetrahedron is chosen so that recursive application to any initial tetrahedron yields elements of at most three congruence classes. Starting from a suitable ordered initial mesh (dividing one cube into six tetrahedron), uniformrefine3 is used in cubemesh.m to produce a uniform mesh of a cube.
Note that sub-tetrahedron may not be always positive ordered.
Refinement
node = [0,0,0; 1,0,0; 1,1,0; 1,1,1];
elem = [1 2 3 4];
figure(1); subplot(1,2,1);
set(gcf,'Units','normal'); set(gcf,'Position',[0.25,0.25,0.5,0.5]);
showmesh3(node,elem,[],'FaceAlpha',0.15); view([34 12]);
findnode3(node);
[node,elem] = uniformrefine3(node,elem);
figure(1); subplot(1,2,2);
showmesh3(node,elem,[],'FaceAlpha',0.15); view([34 12]);
findnode3(node);
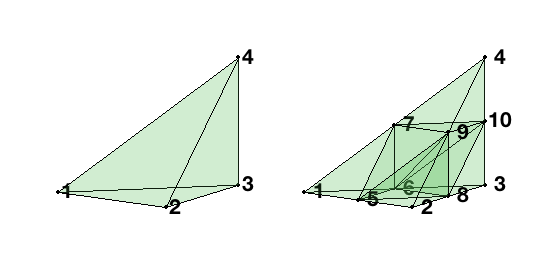
After cutting the four corner, the remaining octahedron should be divided into four tetrahedra by using one of three diagonals. Here follow Bey we always use diagonal 6-9. The ordering of sub-tetrahedron is chosen so that recursive application to any initial tetrahedron yields elements of at most three congruence classes and may not be positive ordered. To get positive ordering, use fixorder3.
[tempvar,idx] = fixorder3(node,elem);
display(idx);
idx =
6
8
The orientation of the 6-th and 8-th children has been changed by fixorder3 which means uniformrefine3 will produces tetrahedrons with negagives volume.
Dependence of the Initial Mesh
node = [1,0,0; 1,1,0; 0,0,0; 1,1,1];
elem = [1 2 3 4];
set(gcf,'Units','normal'); set(gcf,'Position',[0.25,0.25,0.5,0.5]);
figure(1); subplot(1,2,1);
showmesh3(node,elem,[],'FaceAlpha',0.15); view([34 12]);
findnode3(node);
[node,elem] = uniformrefine3(node,elem);
figure(1); subplot(1,2,2);
showmesh3(node,elem,[],'FaceAlpha',0.15); view([34 12]);
findnode3(node);
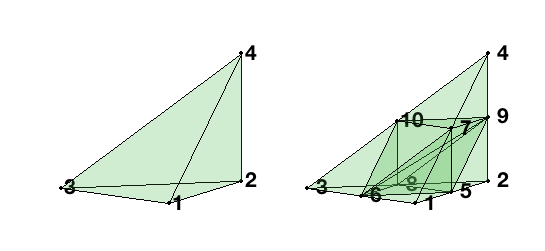
The initial mesh is still positive but after one uniform refinement the diagonal 6-9 is longer than 5-10. Therefore the refined mesh is less shape regular although
still three congruence classes are possible. To have a better mesh quality, one may want to use the shorter one (implemented in uniformrefine3l). The subroutine uniformrefine3
didn’t compute the edge length. The mesh quality will depend on the ordering of the initial mesh.
node = [0,0,0; 1,0,0; 0,1,0; 0,0,1];
elem = [1 2 3 4];
for k = 1:4
[node,elem] = uniformrefine3(node,elem);
meshquality(node,elem);
end
- Min quality 0.6230 - Mean quality 0.7011
- Min quality 0.6230 - Mean quality 0.6934
- Min quality 0.6230 - Mean quality 0.6915
- Min quality 0.6230 - Mean quality 0.6910
We test the quality of meshes obtained by uniformrefine3 for this
initial mesh. The mean of the mesh quality is changing while the
minimial is bounded below.
node = [0,0,0; 1,0,0; 1,1,0; 1,1,1];
elem = [1 2 3 4];
for k = 1:4
[node,elem] = uniformrefine3(node,elem);
meshquality(node,elem);
end
- Min quality 0.7174 - Mean quality 0.7174
- Min quality 0.7174 - Mean quality 0.7174
- Min quality 0.7174 - Mean quality 0.7174
- Min quality 0.7174 - Mean quality 0.7174
If we use the first example, as the correct diagonal used, min=mean which means all elements are in the same type.
Uniform Meshes of a Cube
node = [-1,-1,-1; 1,-1,-1; 1,1,-1; -1,1,-1; -1,-1,1; 1,-1,1; 1,1,1; -1,1,1];
elem = [1 2 3 7; 1 4 3 7; 1 5 6 7; 1 5 8 7; 1 2 6 7; 1 4 8 7];
figure(1); subplot(1,3,1);
showmesh3(node,elem,[],'FaceAlpha',0.25); view([38 10]);
meshquality(node,elem);
[node,elem] = uniformrefine3(node,elem);
figure(1); subplot(1,3,2);
showmesh3(node,elem,[],'FaceAlpha',0.25); view([38 10]);
meshquality(node,elem);
[node,elem] = uniformrefine3(node,elem);
figure(1); subplot(1,3,3);
showmesh3(node,elem,[],'FaceAlpha',0.25); view([38 10]);
meshquality(node,elem);
- Min quality 0.7174 - Mean quality 0.7174
- Min quality 0.7174 - Mean quality 0.7174
- Min quality 0.7174 - Mean quality 0.7174
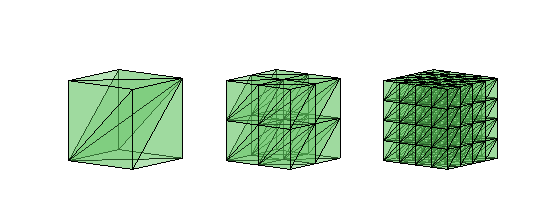
Starting from a suitable ordered initial mesh (dividing one cube into six tetrahedron), uniformrefine3, which is used in cubemesh.m, will produce a
uniform mesh of a cube. In the output of mesh quality, min = mean means all tetrahedron are in one type. Again the obtained tetrahedron may not be all positive ordered.
Test boundary flag
node = [-1,-1,-1; 1,-1,-1; 1,1,-1; -1,1,-1; -1,-1,1; 1,-1,1; 1,1,1; -1,1,1];
elem = [1 2 3 7; 1 4 3 7; 1 5 6 7; 1 5 8 7; 1 2 6 7; 1 4 8 7];
bdFlag = setboundary3(node,elem,'Dirichlet');
for k = 1:2
[node,elem,bdFlag] = uniformrefine3(node,elem,bdFlag);
bdFlagnew = setboundary3(node,elem,'Dirichlet');
display(any(any(bdFlag - bdFlagnew)));
end
ans =
0
ans =
0
bdFlag obtained by uniformrefine3 is the same as bdFlagnew by finding boundary faces of the triangulation.
Reference
- J. Bey. Simplicial grid refinement: on Freudenthal’s algorithm and the
optimal number of congruence classes. Numer. Math. 85(1):1–29, 2000.
p11 Algorithm: RedRefinement3D.
@article{Bey2000, title={Simplicial grid refinement: on Freudenthal's algorithm and the optimal number of congruence classes}, author={Bey, J{\"u}rgen}, journal={Numerische Mathematik}, volume={85}, number={1}, pages={1--29}, year={2000}, publisher={Springer} } - S. Zhang. Successive subdivisions of tetrahedra and multigrid methods
on tetrahedral meshes. Houston J. Math. 21, 541-556, 1995.
@article{Zhang1995, title={Successive subdivisions of tetrahedra and multigrid methods on tetrahedral meshes}, author={Zhang, Shangyou}, journal={Houston J. Math}, volume={21}, number={3}, pages={541--556}, year={1995} }
Comments