Auxiliary Mesh Data Structure
We discuss ways to extract the combinatorial structure of a triangulation by using elem only. Auxiliary data structure includes:
- 2D:
edge, elem2edge, edge2elem, neighbor, bdEdge - 3D:
face, elem2face, face2elem, neighbor, bdFace
They are wrapped into a mesh structure T and can be generated by
T = auxstructure(elem); % 2-D
T = auxstructure3(elem); % 3-D
The auxiliary data structure can be constructed by sparse matrixlization efficiently; see Auxiliary Mesh Data Structure for detailed explanation. In the following, we present a few examples.
edge
We first complete the 2-D simplicial complex represented by elem by constructing its 1-dimensional simplices, i.e., edges of the triangulation. We use edge(1:NE,1:2) to store indices of the starting and ending vertices of edges. The column is sorted in a way such that for the k-th edge, edge(k,1)<edge(k,2). The following code will generate an edge matrix.
[node,elem] = squaremesh([0 1 0 1],0.5);
totalEdge = sort([elem(:,[2,3]); elem(:,[3,1]); elem(:,[1,2])],2);
[i,j,s] = find(sparse(totalEdge(:,2),totalEdge(:,1),1));
edge = [j,i];
bdEdge = [j(s==1),i(s==1)];
showmesh(node,elem);
findedge(node,edge,s==1);
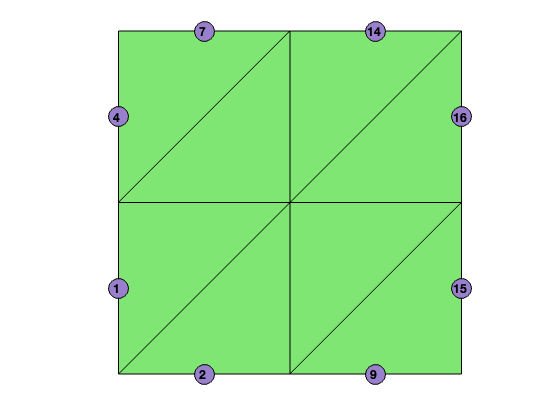
The first line collects all edges from the set of triangles and sorts the column such that totalEdge(k,1)<totalEdge(k,2). The interior edges are repeated twice in totalEdge. We use the summation property of sparse command to merge the duplicated indices. The nonzero vector s takes value 1 (for boundary edges) or 2 (for interior edges). We then use find to return the nonzero indices which forms the edge set. We can also find the boundary edges using the subset of indices pair corresponding to the nonzero value 1. Note that we switch the order of (i,j) in line 3 to sort the edge set row-wise since the output of find(sparse) is sorted column-wise.
To construct edge matrix only, the above 3 line code can be further simplified to one line:
edge = unique(sort([elem(:,[2,3]); elem(:,[3,1]); elem(:,[1,2])],2),'rows');
The unique function provides more functionality which we shall explore more later. However, numerical tests show that the running time of unique is around 3 times of the combination find(sparse()).
node Star
The elem matrix, by the definition, is a pointer from triangles to vertices, i.e., elem is elem2node. The link from vertices to triangles, namely given a vertex, all triangles containing this vertex, can be stored in the sparse matrix t2v:
NT = size(elem,1); N = size(node,1);
t2v = sparse([1:NT,1:NT,1:NT], elem, 1, NT, N);
display(full(t2v));
nodeStar = find(t2v(:,5));
showmesh(node,elem);
findelem(node,elem,nodeStar);
findnode(node,5);
1 0 0 1 1 0 0 0 0
0 1 0 0 1 1 0 0 0
0 0 0 1 0 0 1 1 0
0 0 0 0 1 0 0 1 1
1 1 0 0 1 0 0 0 0
0 1 1 0 0 1 0 0 0
0 0 0 1 1 0 0 1 0
0 0 0 0 1 1 0 0 1
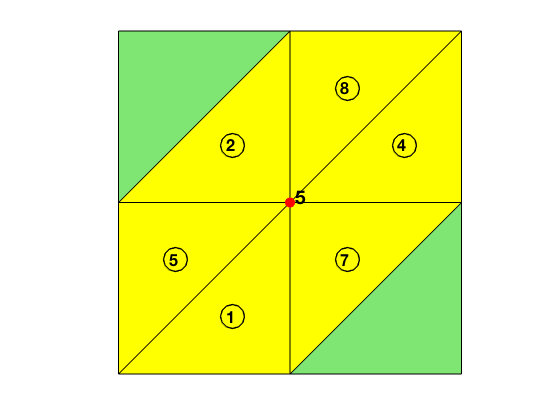
The NT x N matrix t2v is the incidence matrix between triangles and vertices. t2v(t,i)=1 means the i-th node is a vertex of triangle t. If we look at t2v column-wise, the nonzero in the i-th column of t2v(:,i) will give all triangles containing the i-th node. Since a sparse matrix is stored column-wise in MATLAB, the node star of the i-th node can be efficiently found by nodeStar = find(t2v(:,i)).
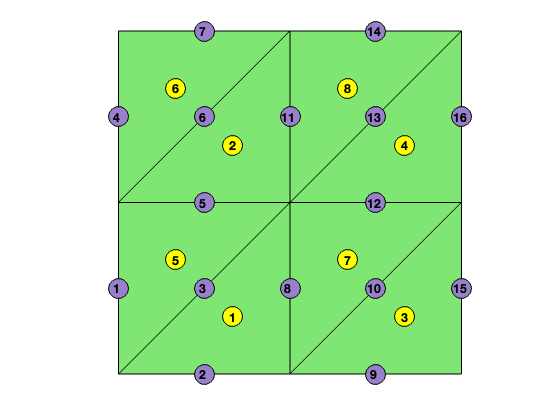
elem2edge
We label three edges of a triangle such that the $i$-th edge is opposite to the $i$-th vertex. We define the matrix elem2edge as the map of the local index of edges in each triangle to its global index. The following 3-line code will construct elem2edge using more output from unique function.
[node,elem] = squaremesh([0 1 0 1],0.5);
totalEdge = sort([elem(:,[2,3]); elem(:,[3,1]); elem(:,[1,2])],2);
[edge, i2, j] = unique(totalEdge,'rows','legacy');
NT = size(elem,1);
elem2edge = reshape(j,NT,3);
Line 1 collects all edges element-wise. The size of totalEdge is thus 3NT x 2. By the construction, there is a natural index mapping from totalEdge to elem. In line 2, we apply unique function to obtain the edge matrix. The output index vectors i2 and j contain the index mapping between edge and totalEdge. Here i2 is an NE x 1 vector to index the last (2-nd in our case) occurrence of each unique value in totalEdge such that edge = totalEdge(i2,:), while j is a 3NT x 1 vector such that totalEdge = edge(j,:). Then using the natural index mapping from totalEdge to elem, we reshape the 3NT x 1 vector j to an NT x 3 matrix which is elem2edge.
Try
help uniquein MATLAB to learn more examples.legacyis used since the version change of MATLAB.
showmesh(node,elem);
findedge(node,edge);
findelem(node,elem);
display(elem2edge);
elem2edge =
3 2 8
6 5 11
10 9 15
13 12 16
3 5 1
6 7 4
10 12 8
13 14 11
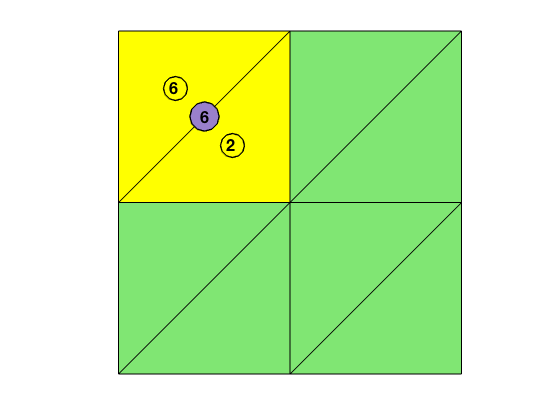
edge2elem
We then define an NE x 4 matrix edge2elem such that edge2elem(k,1) and edge2elem(k,2) are two triangles sharing the k-th edge for an interior edge. If the k-th edge is on the boundary, then we set edge2elem(k,1) = edge2elem(k,2). Furthermore, we shall record the local edge indices in edge2elem(k,3:4) such that elem2edge(edge2elem(k,1),edge2elem(k,3))=k. Namely edge2elem(k,3) is the local index of the k-th edge in edge2elem(k,1) and edge2elem(k,4) is the local index of the k-th edge in edge2elem(k,2).
To construct edge2elem matrix, we need to find out the index map from edge to elem. The following code is a continuation of the code constructing elem2edge.
i1(j(3*NT:-1:1)) = 3*NT:-1:1; i1=i1';
k1 = ceil(i1/NT); t1 = i1 - NT*(k1-1);
k2 = ceil(i2/NT); t2 = i2 - NT*(k2-1);
edge2elem = [t1,t2,k1,k2];
The code in line 1 uses j to find the first occurrence of each unique edge in the totalEdge. In MATLAB, when assign values using an index vector with duplication, the value at the repeated index will be the last one assigned to this location. Obvious j contains duplication of edge indices. For example, j(1)=j(2)=4 which means totalEdge(1,:)=totalEdge(2,:)=edge(4,:). We reverse the ordering of j such that i1(4)=1 which is the first occurrence.
Using the natural index mapping from totalEdge to elem, for an index i between 1:N, the formula k=ceil(i/NT) computes the local index of i-th edge, and t=i-NT*(k-1) is the global index of the triangle which totalEdge(i,:) belongs to. The array edge2elem is just composed by t1,t2,k1 and k2.
showmesh(node,elem);
findelem(node,elem,edge2elem(6,1:2));
findedge(node,edge,6);
display(edge2elem);
edge2elem =
5 5 3 3
1 1 2 2
1 5 1 1
6 6 3 3
2 5 2 2
2 6 1 1
6 6 2 2
1 7 3 3
3 3 2 2
3 7 1 1
2 8 3 3
4 7 2 2
4 8 1 1
8 8 2 2
3 3 3 3
4 4 3 3
Comments