Quadratic Edge Element for Maxwell Equations in 3D

This example is to show the quadratic edge element approximation of the electric field of the time harmonic Maxwell equation.

\[\begin{aligned} \nabla \times (\mu^{-1}\nabla \times u) - \omega^2 \varepsilon \, u &= J \quad \text{ in } \quad \Omega, \\ n \times u &= n \times g_D \quad \text{ on } \quad \Gamma_D, \\ n \times (\mu^{-1}\nabla \times u) &= n \times g_N \quad \text{ on } \quad \Gamma_N. \end{aligned}\]

based on the weak formulation

\[(\mu^{-1}\nabla \times u, \nabla \times v) - (\omega^2\varepsilon u,v) = (J,v) - \langle n \times g_N,v \rangle_{\Gamma_N}.\]

Reference

Subroutines:

  • Maxwell2
  • cubeMaxwell2
  • femMaxwell3
  • Maxwell2femrate

The method is implemented in Maxwell2 subroutine and tested in cubeMaxwell2. Together with other elements (ND0,ND1,ND2), femMaxwell3 provides a concise interface to solve Maxwell equation. The ND1 element is tested in Maxwell2femrate. This doc is based on Maxwell2femrate.

Data Structure

Locally we construct locBasesIdx to record the local index used in the bases. Globally we use ascend ordering for each element and thus the orientation of the edge is consistent. No need of elem2edgeSign. Read Simplicial complex in three dimensions for more discussion of indexing, ordering and orientation.

In addition to the edge structure, we need face and the corresponding pointers.

[node,elem] = cubemesh([0,1,0,1,0,1],1);
[elem2edge,edge] = dof3edge(elem);
[elem2face,face] = dof3face(elem);

Furthermore we need pointer from face to edge. face is given by auxtructure3 and is sorted according to global indices. face2edge is used to compute uI. So it is consistent with the local index system in edgeinterpolate2, i.e., if face is (i,j,k) with i<j<k, then the three edges are [i j], [i k], [j k].

face2edge = zeros(size(face,1),3,'int32');
face2edge(elem2face(:,1),:) = elem2edge(:,[4 5 6]);
face2edge(elem2face(:,2),:) = elem2edge(:,[2 3 6]);
face2edge(elem2face(:,3),:) = elem2edge(:,[1 3 5]);
face2edge(elem2face(:,4),:) = elem2edge(:,[1 2 4]);

locEdge = [1 2; 1 3; 1 4; 2 3; 2 4; 3 4];
locFace = [2 3 4; 1 3 4; 1 2 4; 1 2 3];
locBasesIdx = [1 2 0; 1 3 0; 1 4 0; 2 3 0; 2 4 0; 3 4 0; ... % phi
               1 2 0; 1 3 0; 1 4 0; 2 3 0; 2 4 0; 3 4 0; ... % psi
               3 2 4; 3 1 4; 2 1 4; 2 1 3; ...
               4 2 3; 4 1 3; 4 1 2; 3 1 2]; % chi

Locally we construct locBasesIdx to record the local index used in the bases. For example, for basis $\chi_i =\lambda_{i_1}\phi _{i_2i_3}$ for i=4, we can get i1,i2,i3 by:

i = 4+12;
i1 = locBasesIdx(i,1); i2 = locBasesIdx(i,2); i3 = locBasesIdx(i,3);

Local Bases

Suppose [i,j] is the kth edge and i<j. The basis is given by

\[\phi _k = \lambda_i\nabla \lambda_j - \lambda_j \nabla \lambda_i,\qquad \nabla \times \phi_k = 2\nabla \lambda_i \times \nabla \lambda_j.\]

Inside one tetrahedron, the 6 bases functions along with their curl corresponding to 6 local edges [1 2; 1 3; 1 4; 2 3; 2 4; 3 4] are

\[\phi_1 = \lambda_1\nabla\lambda_2 - \lambda_2\nabla\lambda_1,\qquad \nabla \times \phi_1 = 2\nabla\lambda_1\times \nabla\lambda_2,\] \[\phi_2 = \lambda_1\nabla\lambda_3 - \lambda_3\nabla\lambda_1,\qquad \nabla \times \phi_2 = 2\nabla\lambda_1\times \nabla\lambda_3,\] \[\phi_3 = \lambda_1\nabla\lambda_4 - \lambda_4\nabla\lambda_1,\qquad \nabla \times \phi_3 = 2\nabla\lambda_1\times \nabla\lambda_4,\] \[\phi_4 = \lambda_2\nabla\lambda_3 - \lambda_3\nabla\lambda_2,\qquad \nabla \times \phi_4 = 2\nabla\lambda_2\times \nabla\lambda_3,\] \[\phi_5 = \lambda_2\nabla\lambda_4 - \lambda_4\nabla\lambda_2,\qquad \nabla \times \phi_5 = 2\nabla\lambda_2\times \nabla\lambda_4,\] \[\phi_6 = \lambda_3\nabla\lambda_4 - \lambda_4\nabla\lambda_3,\qquad \nabla \times \phi_6 = 2\nabla\lambda_3\times \nabla\lambda_4.\]

The additional 6 bases for the second family are:

\[\psi_k = \lambda_i\nabla \lambda_j + \lambda_j \nabla \lambda_i,\qquad \nabla \times \psi_k = 0.\] \[\psi_1 = \lambda_1\nabla\lambda_2 + \lambda_2\nabla\lambda_1,\] \[\psi_2 = \lambda_1\nabla\lambda_3 + \lambda_3\nabla\lambda_1,\] \[\psi_3 = \lambda_1\nabla\lambda_4 + \lambda_4\nabla\lambda_1,\] \[\psi_4 = \lambda_2\nabla\lambda_3 + \lambda_3\nabla\lambda_2,\] \[\psi_5 = \lambda_2\nabla\lambda_4 + \lambda_4\nabla\lambda_2,\] \[\psi_6 = \lambda_3\nabla\lambda_4 + \lambda_4\nabla\lambda_3.\]

Suppose i,j,k are the vertices of the l-th face and i<j<k. The two basis associated to this face are

\[\chi_l^1 = \lambda_j\phi _{ik} = \lambda_j(\lambda_i\nabla\lambda_k - \lambda_k\nabla\lambda_i),\quad \chi_l^2 = \lambda_k\phi _{ij} = \lambda_k(\lambda_i\nabla\lambda_j - \lambda_j\nabla\lambda_i).\]

Inside one tetrahedron, the 8 bases functions assocaited to the four local faces [2 3 4; 1 3 4; 1 2 4; 1 2 3] are:

\[\chi_1^1 = \lambda_3\phi _{24} = \lambda_3(\lambda_2\nabla\lambda_4 - \lambda_4\nabla\lambda_2),\quad \chi_1^2 = \lambda_4\phi _{23} = \lambda_4(\lambda_2\nabla\lambda_3 - \lambda_3\nabla\lambda_2).\] \[\chi_2^1 = \lambda_3\phi _{14} = \lambda_3(\lambda_1\nabla\lambda_4 - \lambda_4\nabla\lambda_1),\quad \chi_2^2 = \lambda_4\phi _{13} = \lambda_4(\lambda_1\nabla\lambda_3 - \lambda_3\nabla\lambda_1).\] \[\chi_3^1 = \lambda_2\phi _{14} = \lambda_2(\lambda_1\nabla\lambda_4 - \lambda_4\nabla\lambda_1),\quad \chi_3^2 = \lambda_4\phi _{12} = \lambda_4(\lambda_1\nabla\lambda_2 - \lambda_2\nabla\lambda_1).\] \[\chi_4^1 = \lambda_2\phi _{13} = \lambda_2(\lambda_1\nabla\lambda_3 - \lambda_3\nabla\lambda_1),\quad \chi_4^2 = \lambda_3\phi _{12} = \lambda_3(\lambda_1\nabla\lambda_2 - \lambda_2\nabla\lambda_1).\]

Reference: See page 12, Table 9.2. Arnold, Douglas N. and Falk, Richard S. and Winther, Ragnar. Geometric decompositions and local bases for spaces of finite element differential forms. Comput. Methods Appl. Mech. Engrg. 198():1660–1672, 2009.

Locally, we order the local bases in the following way:

\[\{\chi_1^1,~\,\chi_1^2,~\,\chi_2^1,~\,\chi_2^2,~\,\chi_3^1,~\,\chi_3^2, ~\,\chi_4^1,~\,\chi_4^2.\}\]

and rewrite the local bases as:

13- 20: \(\{\chi_1,~\,\chi_2,~\,\chi_3,~\,\chi_4,~\,\chi_5,~\,\chi_6,~\, \chi_7,~\,\chi_8.\}\)

Degree of freedoms

Suppose [i,j] is the kth edge and i<j. The corresponding degree of freedom is

\[l_k (v) = \int_{e_k} v\cdot t \, {\rm d}s \approx \frac{1}{2}[v(i)+v(j)]\cdot e_{k}.\]

It is dual to the basis ${\phi_k}$ in the sense that

\[l_{\ell}(\phi _k) = \delta_{k,\ell}.\]

The 6 degree of freedoms for $\psi_k$ are:

\[l_k^1 (v) = 3\int_{e_k} v\cdot t(\lambda _i - \lambda_j) \, {\rm d}s \approx \frac{1}{2}[v(i) - v(j)]\cdot e_{k}.\]

The 8 degree of freedoms for $\chi_i$ is given in edgeinterpolate2.

Dirichlet boundary condition

%% Setting
[node,elem] = cubemesh([-1,1,-1,1,-1,1],1);
mesh = struct('node',node,'elem',elem);
option.L0 = 0;
option.maxIt = 4;
option.elemType = 'ND2';
option.printlevel = 1;
option.plotflag = 1;
imatlab_export_fig('print-png')  % Static png figures.

%% Dirichlet boundary condition.
fprintf('Dirichlet boundary conditions. \n');    
pde = Maxwelldata2;
bdFlag = setboundary3(node,elem,'Dirichlet');
femMaxwell3(mesh,pde,option);

Dirichlet boundary conditions. 
Conjugate Gradient Method using HX preconditioner 
#dof:    21424,   #nnz:   639262,   iter: 39,   err = 7.7689e-09,   time = 0.59 s
Conjugate Gradient Method using HX preconditioner 
#dof:   163424,   #nnz:  5701026,   iter: 40,   err = 8.8053e-09,   time =  4.7 s
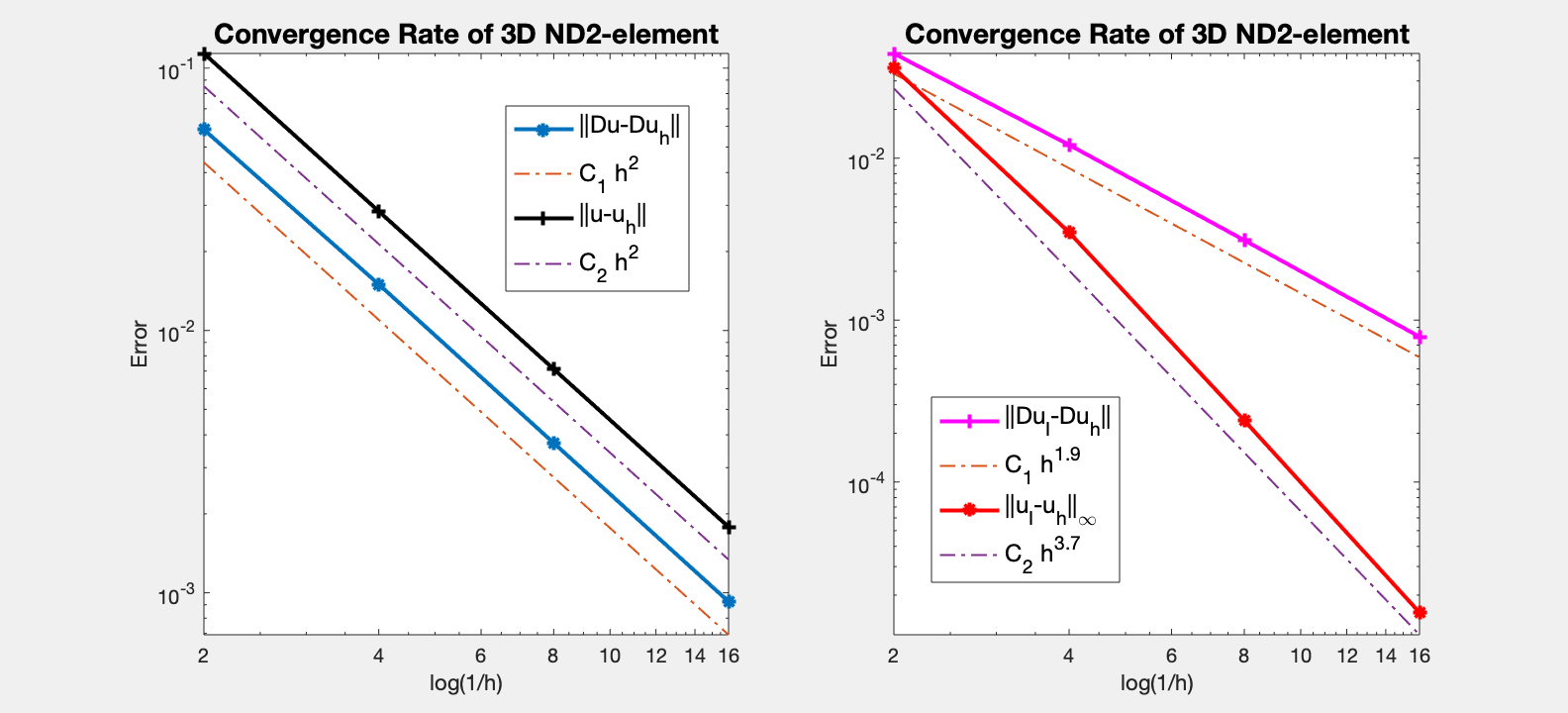
Table: Error
 #Dof        h        ||u-u_h||    ||Du-Du_h||   ||DuI-Du_h|| ||uI-u_h||_{max}

   436   5.000e-01   1.13740e-01   5.82980e-02   4.43112e-02   3.59660e-02
  2936   2.500e-01   2.84527e-02   1.49856e-02   1.20812e-02   3.47958e-03
 21424   1.250e-01   7.12530e-03   3.72448e-03   3.11254e-03   2.39778e-04
163424   6.250e-02   1.78245e-03   9.25140e-04   7.88591e-04   1.56095e-05

Table: CPU time
 #Dof    Assemble     Solve      Error      Mesh    

   436   1.20e-01   1.20e-01   4.00e-02   1.00e-02
  2936   1.40e-01   1.70e-01   5.00e-02   1.00e-02
 21424   6.70e-01   5.90e-01   3.70e-01   2.00e-02
163424   3.67e+00   4.68e+00   1.38e+00   5.00e-02

png

Neumann Boundary Condition

fprintf('Neumann boundary condition. \n');
option.plotflag = 0;
pde = Maxwelldata2;
mesh.bdFlag = setboundary3(node,elem,'Neumann');
femMaxwell3(mesh,pde,option);

Neumann boundary condition. 
#dof:      436, Direct solver 0.07 
#dof:     2936, Direct solver 0.12 
Conjugate Gradient Method using HX preconditioner 
#dof:    21424,   #nnz:   812592,   iter: 48,   err = 9.8413e-09,   time = 0.81 s
Conjugate Gradient Method using HX preconditioner 
#dof:   163424,   #nnz:  6416872,   iter: 48,   err = 7.9588e-09,   time =  6.5 s
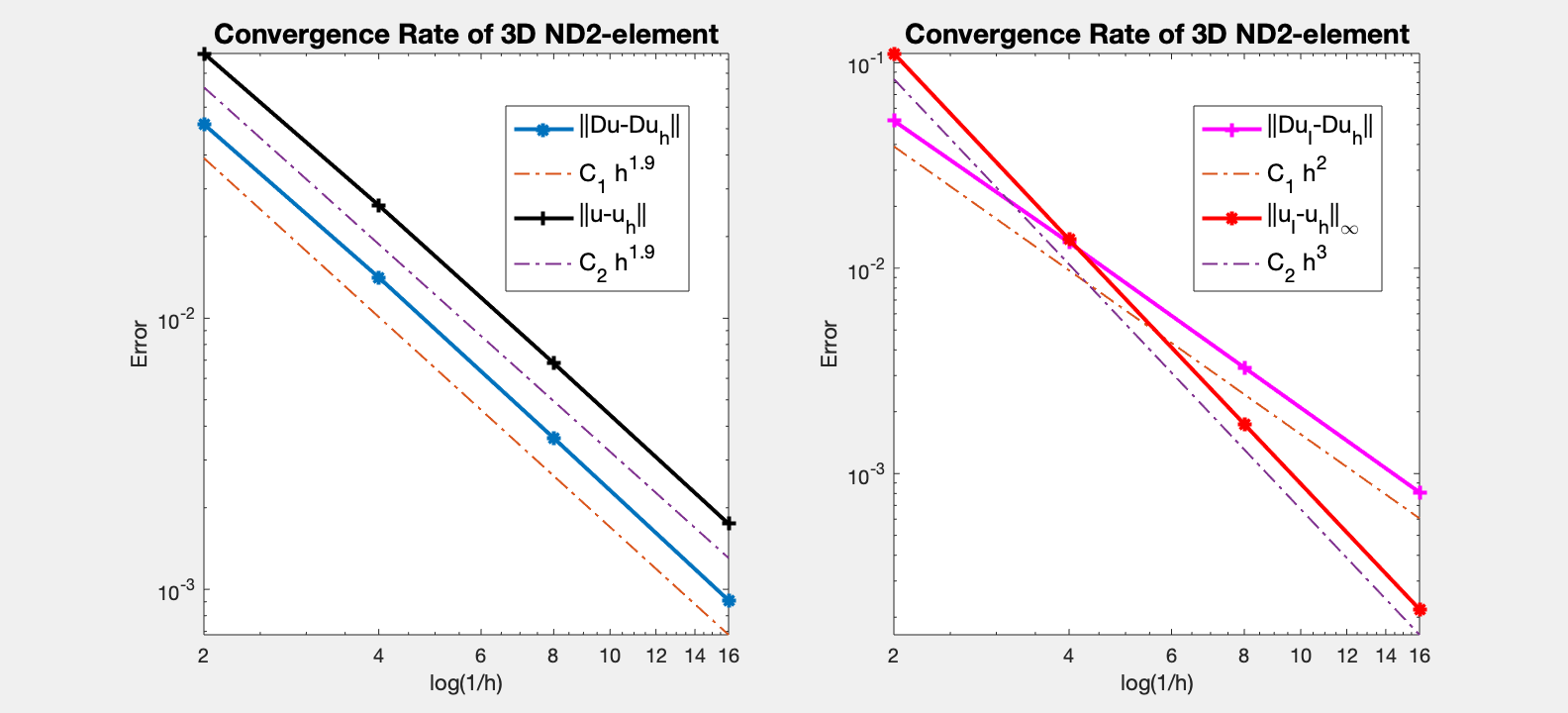
Table: Error
 #Dof        h        ||u-u_h||    ||Du-Du_h||   ||DuI-Du_h|| ||uI-u_h||_{max}

   436   5.000e-01   9.46920e-02   5.19223e-02   5.21912e-02   1.10980e-01
  2936   2.500e-01   2.60741e-02   1.41384e-02   1.33189e-02   1.37866e-02
 21424   1.250e-01   6.82809e-03   3.61596e-03   3.28025e-03   1.74118e-03
163424   6.250e-02   1.74533e-03   9.11412e-04   8.10177e-04   2.18397e-04

Table: CPU time
 #Dof    Assemble     Solve      Error      Mesh    

   436   6.00e-02   7.00e-02   2.00e-02   0.00e+00
  2936   9.00e-02   1.20e-01   4.00e-02   0.00e+00
 21424   4.60e-01   8.10e-01   2.70e-01   1.00e-02
163424   2.87e+00   6.53e+00   1.34e+00   4.00e-02

png

Conclusion

Both the H(curl)-norm and the L2-norm is 2nd order.

MGCG using HX preconditioner converges uniformly in all cases.

Comments