RT0-P0 Element for Poisson Equation in 3D
This example is to show the rate of convergence of the linear finite element approximation of the Poisson equation on the unit square:
\[- \nabla (d \nabla) u = f \; \hbox{in } (0,1)^2\]for the following boundary conditions
- pure Dirichlet boundary condition: $u = g_D \text{ on } \partial \Omega$.
- Pure Neumann boundary condition: $d\nabla u\cdot n=g_N \text{ on } \partial \Omega$.
- mixed boundary condition: $u=g_D \text{ on }\Gamma_D, \nabla u\cdot n=g_N \text{ on }\Gamma_N.$
Find $(\sigma , u)$ in $H_{g_N,\Gamma_N}(div,\Omega)\times L^2(\Omega)$ s.t.
\[(d^{-1}\sigma,\tau) + (\mathrm{div}\, \tau, u) = \langle \tau \cdot n, g_D \rangle_{\Gamma_D} \quad \forall \tau \in H_{0,\Gamma_N}(div,\Omega)\] \[(\mathrm{div}\, \sigma, v) = -(f,v) \quad \forall v \in L^2(\Omega)\]where
\[H_{g,\Gamma}(\mathrm{div},\Omega) = \{\sigma \in H(\mathrm{div}; \sigma \cdot n = g \text{ on } \Gamma \subset \partial\Omega \}.\]The unknown $\sigma = d\nabla u$ is approximated using the lowest order Raviart-Thomas element (RT0) and $u$ by piecewise constant element (P0).
References
Subroutines:
- Poisson3RT0
- cubePoisson3RT0
- mfemPoisson3
- Poisson3RT0mfemrate
The method is implemented in Poisson3RT0 subroutine and tested in cubePoisson3RT0. Together with other elements (BDM1), mfemPoisson provides a concise interface to solve Poisson equation in mixed formulation. The RT0-P0 element is tested in Poisson3RT0mfemrate. This doc is based on Poisson3RT0mfemrate.
RT0 Lowest Order H(div) Element in 3D
We explain degree of freedoms and basis functions for Raviart-Thomas element on a triangle.
Asecond orientation
The dofs and basis depends on the orientation of the mesh. We shall use the asecond orientation, i.e., elem(t,1)< elem(t,2)< elem(t,3)< elem(t,4) not the positive orientation. Given an elem, the asecond orientation can be constructed by
[elem,bdFlag] = sortelem(elem,bdFlag); % ascend ordering
Note that bdFlag should be sorted as well.
The local face is also asecond [2 3 4; 1 3 4; 1 2 4; 1 2 3] so that the local orientation is consistent with the global one and thus no need to deal with the sign difference when the positive oritentation is used. Read Simplicial complex in three dimensions for more discussion of indexing, ordering and orientation.
node = [1,0; 1,1; 0,0];
elem = [1 2 3];
edge = [2 3; 1 3; 1 2];
figure;
subplot(1,2,1)
showmesh(node,elem);
findnode(node);
findedge(node,edge,'all','rotvec');
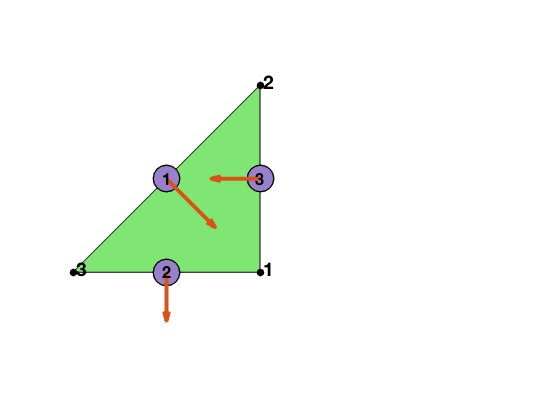
Local bases of RT0 element
Suppose $i,j,k$ are the vertices of the $l$-th face. The basis associated the face is given by
\[\phi_l = 2(\lambda_i\nabla \lambda_j \times \nabla\lambda_k + \lambda_j\nabla \lambda_k \times \nabla\lambda_i + \lambda_k\nabla \lambda_i \times \nabla\lambda_j).\]Inside one tetrahedron, the 4 bases functions corresponding to 4 local faces [2 3 4; 1 3 4; 1 2 4; 1 2 3] are:
\[\phi_1 = 2(\lambda_2\nabla \lambda_3 \times \nabla\lambda_4 + \lambda_3\nabla \lambda_4 \times \nabla\lambda_2 + \lambda_4\nabla \lambda_2 \times \nabla\lambda_3).\] \[\phi_2 = 2(\lambda_1\nabla \lambda_4 \times \nabla\lambda_3 + \lambda_4\nabla \lambda_1 \times \nabla\lambda_3 + \lambda_3\nabla \lambda_1 \times \nabla\lambda_4).\] \[\phi_3 = 2(\lambda_1\nabla \lambda_2 \times \nabla\lambda_4 + \lambda_2\nabla \lambda_4 \times \nabla\lambda_1 + \lambda_4\nabla \lambda_1 \times \nabla\lambda_2).\] \[\phi_4 = 2(\lambda_1\nabla \lambda_3 \times \nabla\lambda_2 + \lambda_3\nabla \lambda_2 \times \nabla\lambda_1 + \lambda_2\nabla \lambda_1 \times \nabla\lambda_3).\]As for the computation of the integration of divergence of the basis, We have the following good property.
\[\int_t \phi_i = dofSign(t,i)\]This property can be drived from relationship between Whitney forms. Say the following:
\[grad w_n = \sum_{e\in patch of n}G_{en}w_e, \qquad curl w_e = \sum_{f\in patch of e}C_{fe}w_f, \qquad div w_f = \sum_{t\in patch of f}D_{tf}w_t\]where $w_n, w_e, w_f, w_t$ are nodal element basis, edge element basis, face element basis, and volume element basis respectively. As for the volume element (or tetrahedral) basis,
\[w_t = 1/v(t) \hbox{ on t and 0 otherwise }.\]Because of the different oritentation of local and global faces, from local bases to the global one, the direction should be corrected. That is
phiGlobal(elem2dof(t,1),:) = phi(t,1)*dofSign(t,1);
Local to global index map
Three local edges are locEdge = [2 3; 1 3; 1 2]. The pointer from the local to global index can be constructured by
[elem2dof,edge] = dofedge(elem);
[node,elem] = squaremesh([0 1 0 1], 0.5);
bdFlag = setboundary(node,elem,'Dirichlet');
[elem,bdFlag] = sortelem(elem,bdFlag);
showmesh(node,elem);
findnode(node);
findelem(node,elem);
[elem2dof,edge] = dofedge(elem);
findedge(node,edge,'all','rotvec');
display(elem2dof);
elem2dof =
8�3 uint32 matrix
8 3 2
11 6 5
15 10 9
16 13 12
5 3 1
7 6 4
12 10 8
14 13 11
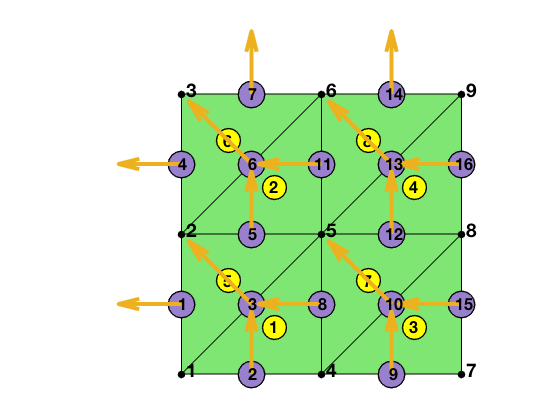
Assembling the matrix equation
We discuss several issues in the assembling.
Mass matrix
The mass matrix can be computed by
M = getmassmatvec(elem2edge,area,Dlambda,'RT0');
divergence matrix
The ascend ordering orientation is not consistent with the induced orientation. The second edge would be [3 1] for the consistent orientation. So [1 -1 1] is used in the construction of div operator.
For triangle t, the basis for the constant function space is $p = 1$, the characteristic function. So in the computation of divergence operator, elemSign should be used to correct the sign. In the output of gradbasis, -Dlambda is always the outwards normal direction. The signed area could be negative but in the ouput, area is the absolute value (for the easy of integration on elements) and elemSign is used to record elements with negative area.
[Dlambda,area,elemSign] = gradbasis(node,elem);
B = icdmat(double(elem2dof),elemSign*[1 -1 1]);
display(full(B))
Columns 1 through 13
0 1 -1 0 0 0 0 1 0 0 0 0 0
0 0 0 0 1 -1 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 1 -1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 -1
-1 0 1 0 -1 0 0 0 0 0 0 0 0
0 0 0 -1 0 1 -1 0 0 0 0 0 0
0 0 0 0 0 0 0 -1 0 1 0 -1 0
0 0 0 0 0 0 0 0 0 0 -1 0 1
Columns 14 through 16
0 0 0
0 0 0
0 1 0
0 0 1
0 0 0
0 0 0
0 0 0
-1 0 0
Boundary edges
Direction of boundary edges may not be the outwards normal direction of the domain since now elem is ascend orientation. edgeSign is introduced to record this inconsistency.
edgeSign = ones(NE,1);
idx = (bdFlag(:,1) ~= 0) & (elemSign == -1); % first edge is on boundary
edgeSign(elem2edge(idx,1)) = -1;
idx = (bdFlag(:,2) ~= 0) & (elemSign == 1); % second edge is on boundary
edgeSign(elem2edge(idx,2)) = -1;
idx = (bdFlag(:,3) ~= 0) & (elemSign == -1); % third edge is on boundary
edgeSign(elem2edge(idx,3)) = -1;
Test Examples
Mixed boundary condition
%% Setting
[node,elem] = squaremesh([0,1,0,1],0.25);
mesh = struct('node',node,'elem',elem);
option.L0 = 1;
option.maxIt = 4;
option.printlevel = 1;
option.elemType = 'RT0';
pde = sincosNeumanndata;
%% Mix Dirichlet and Neumann boundary condition.
option.solver = 'uzawapcg';
mesh.bdFlag = setboundary(node,elem,'Dirichlet','~(x==0)','Neumann','x==0');
mfemPoisson(mesh,pde,option);
Uzawa-type MultiGrid Preconditioned PCG
#dof: 336, #nnz: 1200, V-cycle: 1, iter: 16, err = 6.10e-09, time = 0.44 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 1312, #nnz: 4832, V-cycle: 1, iter: 16, err = 7.58e-09, time = 0.1 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 5184, #nnz: 19392, V-cycle: 1, iter: 16, err = 9.33e-09, time = 0.17 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 20608, #nnz: 77696, V-cycle: 1, iter: 16, err = 9.13e-09, time = 0.51 s
#Dof h ||u-u_h|| ||u_I-u_h|| ||sigma-sigma_h||||sigma-sigma_h||_{div}
336 1.25e-01 1.29904e-01 3.24734e-02 1.00431e+00 1.01710e+01
1312 6.25e-02 6.53343e-02 8.36322e-03 5.03316e-01 5.14701e+00
5184 3.12e-02 3.27108e-02 2.10609e-03 2.51787e-01 2.58126e+00
20608 1.56e-02 1.63607e-02 5.27476e-04 1.25909e-01 1.29160e+00
#Dof Assemble Solve Error Mesh
336 1.20e-01 4.40e-01 1.20e-01 2.00e-02
1312 1.00e-01 1.00e-01 1.00e-01 1.00e-02
5184 1.00e-01 1.70e-01 6.00e-02 1.00e-02
20608 7.00e-02 5.10e-01 1.20e-01 2.00e-02
Pure Neumann boundary condition
In mixed formulation,the Neumann boundary condition for $d\nabla u$ becomes the Dirichlet boundary condiiton for $\sigma$. The space for $u$ is $L^2_0$ and thus one dof should be removed to have a non-singular system.
option.plotflag = 0;
mesh.bdFlag = setboundary(node,elem,'Neumann');
mfemPoisson(mesh,pde,option);
Uzawa-type MultiGrid Preconditioned PCG
#dof: 336, #nnz: 1102, V-cycle: 1, iter: 16, err = 3.20e-09, time = 0.15 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 1312, #nnz: 4638, V-cycle: 1, iter: 17, err = 3.67e-09, time = 0.04 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 5184, #nnz: 19006, V-cycle: 1, iter: 18, err = 3.25e-09, time = 0.19 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 20608, #nnz: 76926, V-cycle: 1, iter: 18, err = 8.29e-09, time = 0.47 s
#Dof h ||u-u_h|| ||u_I-u_h|| ||sigma-sigma_h||||sigma-sigma_h||_{div}
336 1.25e-01 1.35274e-01 4.88517e-02 1.00659e+00 1.01710e+01
1312 6.25e-02 6.55354e-02 1.00318e-02 5.03633e-01 5.14701e+00
5184 3.12e-02 3.27194e-02 2.33376e-03 2.51827e-01 2.58126e+00
20608 1.56e-02 1.63613e-02 5.71884e-04 1.25914e-01 1.29160e+00
#Dof Assemble Solve Error Mesh
336 6.00e-02 1.50e-01 3.00e-02 0.00e+00
1312 1.00e-02 4.00e-02 2.00e-02 0.00e+00
5184 2.00e-02 1.90e-01 4.00e-02 0.00e+00
20608 5.00e-02 4.70e-01 1.00e-01 1.00e-02
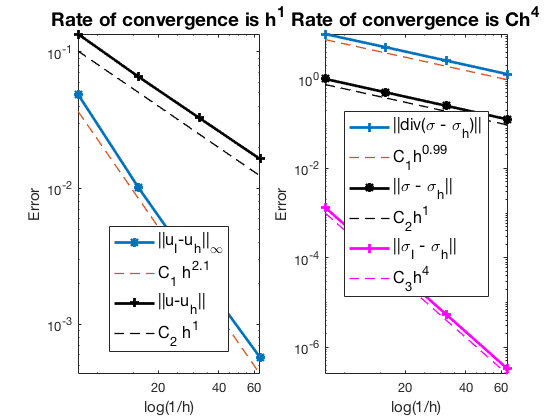
Pure Dirichlet boundary condition
%% Pure Dirichlet boundary condition.
mesh.bdFlag = setboundary(node,elem,'Dirichlet');
mfemPoisson(mesh,pde,option);
Uzawa-type MultiGrid Preconditioned PCG
#dof: 336, #nnz: 1232, V-cycle: 1, iter: 16, err = 3.60e-09, time = 0.09 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 1312, #nnz: 4896, V-cycle: 1, iter: 16, err = 6.53e-09, time = 0.05 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 5184, #nnz: 19520, V-cycle: 1, iter: 16, err = 8.34e-09, time = 0.16 s
Uzawa-type MultiGrid Preconditioned PCG
#dof: 20608, #nnz: 77952, V-cycle: 1, iter: 16, err = 8.49e-09, time = 0.43 s
#Dof h ||u-u_h|| ||u_I-u_h|| ||sigma-sigma_h||||sigma-sigma_h||_{div}
336 1.25e-01 1.29702e-01 3.08718e-02 1.00257e+00 1.01710e+01
1312 6.25e-02 6.53059e-02 7.92226e-03 5.03081e-01 5.14701e+00
5184 3.12e-02 3.27071e-02 1.99320e-03 2.51757e-01 2.58126e+00
20608 1.56e-02 1.63602e-02 4.99086e-04 1.25905e-01 1.29160e+00
#Dof Assemble Solve Error Mesh
336 1.00e-02 9.00e-02 1.00e-02 0.00e+00
1312 0.00e+00 5.00e-02 1.00e-02 0.00e+00
5184 2.00e-02 1.60e-01 3.00e-02 1.00e-02
20608 5.00e-02 4.30e-01 1.00e-01 1.00e-02

Conclusion
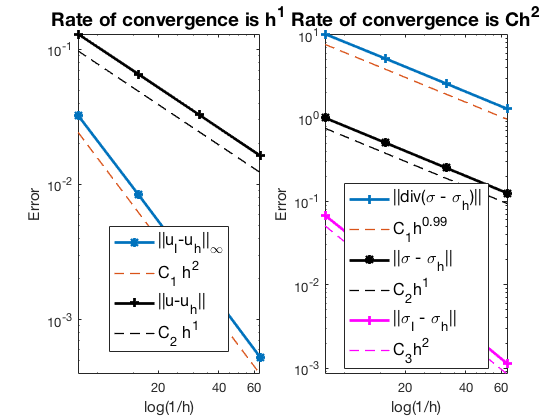
The optimal rates of convergence for $u$ and $\sigma$ are observed, namely, 1st order for L2 norm of u, L2 norm of $\sigma$ and H(div) norm of $\sigma$. The 2nd order convergent rates between two discrete functions $|u_I - u_h|$ and $|\sigma_I - \sigma_h|$ are known as superconvergence.
Triangular preconditioned GMRES (the default solver) and Uzawa preconditioned CG converges uniformly in all cases. Traingular preconditioner is two times faster than PCG although GMRES is used.
Comments